Geordnetes Paar

Dieser Artikel erfüllt die GlossarWiki-Qualitätsanforderungen nur teilweise:

Korrektheit: 3 (zu größeren Teilen überprüft)

Umfang: 3 (einige wichtige Fakten fehlen)

Quellenangaben: 5 (vollständig vorhanden)

Quellenarten: 5 (ausgezeichnet)

Konformität: 5 (ausgezeichnet)

Es fehlen wichtige Fakten zur Geschichte des Begriffes.

Ein geordnetes Paar $(a,b)$ bezeichnet die Zusammenfassung zweier nicht notwendigerweise verschiedener Objekte $a$ und $b$ zu einer Einheit. Die beiden Objekte sind dabei angeordnet. Das heißt, die beiden Paare $(a,b)$ und $(b,a)$ sind dann und nur dann gleich, wenn $a$ und $b$ gleich sind.

„Geordnetes Paar“ ist ein elementarer Grundbegiff und ein zentrales Hilfsmittel der Mathematik und der Informatik, um Beziehungen zwischen Objekten beschreiben zu können, d. h., um Relationen und Funktionen oder andere komplexe Datenstrukturen definieren zu können.

Vorbemerkung

Im alltäglichen Leben trifft man auf zwei Arten von Paaren: ungeordnete und geordnete Paare. Beispielsweise handelt es sich bei einem üblichen Paar Socken um ein ungeordnetes Paar (es ist egal, welche Socke man links und welche rechts anzieht), ein Paar Schuhe ist dagegen geordnet. Ehepaare sind – zumindest im aktuellen deutschen Rechtssystem – ungeordnet (auch wenn mir kein behördliches Formular bekannt ist, auf dem die Ehefrau vor dem Ehemann genannt wird), noch mehr trifft dies auf gleichgeschlechtliche Partnerschaften zu. Mutter-Kind-/Vater-Kind-Beziehungen sind dagegen geordnet. Etc. pp.

In der Mathematik unterscheidet man ebenfalls zwischen ungeordneten und geordneten Paaren. Bei „ungeordneten Paaren“ (Paarmengen) $\{a,b\}$ sind nur die Elemente von Bedeutung, die Reihenfolge der Elemente spielt dagegen keine Rolle:

Die Paarmengen $\{a,b\}$ und $\{b,a\}$ sind für alle Elemente $a$ und $b$ gleich.

$\bigwedge a,b:\{a,b\}=\{b,a\}$

Damit es sich bei „ungeordneten Paaren“ wirklich um Paare handelt, muss man $a\ne b$ fordern, da $\{a,a\}=\{a\}$ eine einelementige Menge ist.

Im Gegensatz dazu sind bei „geordneten Paaren“ $[a,b]$ (wobei auch $a=b$ erlaubt ist) nicht nur deren Elemente von Bedeutung, sondern zusätzlich noch deren Reihenfolge:

Die geordneten Paare $[a,b]$ und $[b,a]$ sind dann und nur dann gleich, wenn $a$ gleich $b$ ist.

$\bigwedge a,b:[a,b]=[b,a]\leftrightarrow a=b$

Paaraxiom von Hamilton, Hamilton (1837), S. 300

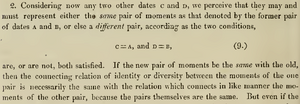
Das Paaraxiom (genauer: das Gleichheitsaxiom für geordnete Paare) von Hamilton lautet:

Zwei geordnete Paare $[a,b]$ und $[c,d]$ sind genau gleich, wenn $a$ gleich $c$ und $b$ gleich $d$ ist.

$\bigwedge a,b:[a,b]=[c,d]\leftrightarrow a=c\wedge b=d$

Es garantiert, dass stets entschieden werden kann, welches das erste und welches das zweite Element eines geordneten Paares ist.

Geordnete Paare und deren Verallgemeinerung, die Tupel, sind sowohl in der Mathematik als auch in der Informatik von zentraler Bedeutung:

• In der Analysis werden sie verwendet, um beispielsweise ganze Zahlen, rationale Zahlen, komplexe Zahlen oder Quaternionen zu definieren.
• In der Geometrie kommen sie zum Einsatz, um mehrdimensionale Räume (insbesondere Vektorräume) zu beschreiben.
• In der Mengenlehre definiert man mit ihrer Hilfe Relationen und Funktionen.
• In LISP sind geordnet Paare die zentrale Datenstruktur, mit deren Hilfe alle komplexen Elemente (Listen und Lambda-Operationen) der Sprache realisiert werden.
• Relationen, d. h. Mengen (und Multimengen) von Tupeln, sind die zentrale Datenstruktur von relationalen Datenbanken.
• Viele komplexe Datenstrukturen der Informatik basieren auf geordneten Paaren und Tupeln: verkettete Listen, Bäume, gerichtete Graphen, Objekte etc.

Die Geschichte der Definition des Begriffs „geordnetes Paar“ ist erstaunlich komplex. Zum einen besteht ein inhärentes Henne-Ei-Problem: Es ist nicht möglich, einen Ordnungsbegriff zu definieren, wenn man nicht schon einen Ordnungsbegriff hat. Wenn man beispielsweise das geordnete Paar mit Hilfe von Mengen, d. h. mit Hilfe des Elementoperators $\in$ definiert, verwendet man einen Operator, der selbst schon zwei Elemente anordnet: $a\in b$ bedeutet etwas anderes als $b\in a$. Diese Problem ist philosophischer Natur und besteht in der Mathematik prinzipiell. Um eine Objektsprache zu definieren, benötigt man eine Metasprache, in der viele der auf Objektebene zu definierenden oder zu beweisenden Eigenschaften schon als gültig angesehen werden. Zur Definition der Metasprache benötigt man eine Metametasprache etc. pp.

Das zweite große Problem der Paar-Definition ist, dass jede Rückführung des Begriffs auf schon bekannte Begriffe den Paaren zusätzliche Eigenschaften beschert, die eigentlich nichts mit dem Paarbegriff an sich zu tun haben, sondern nur mit der jeweiligen Definition. Die wesentliche Frage ist nun: Welche Eigenschaften sind vorteilhaft? Welche Eigenschaften sind nachteilig? Welches ist für die jeweilige Anwendung die beste Definition? Auch diese Fragen lassen sich nicht abschließend klären, sondern hängen vom jeweiligen Anwendungsfall ab.

Container

In der Mathemtik und der Informatik ist es von fundamentaler Bedeutung, bestimmte Objekte zu größeren Einheiten zusammenzufassen. In diesem Wiki werden Objekte, die andere Objekte enthalten können, als Container bezeichnet und Objekte, die in Containern enthalten sein können, als Elemente.

Geordnete Paare sind per Definitionem Container, da sie genau zwei Objekte als Elemente enthalten, die so genannten Paarelemente. Auch die Verallgemeinerung der geordneten Paare, die Tupel sind Container. Ein $n$-Tupel enthält genau $n$ Elemente – die so genannten Tupelelemente – in einer bestimmten Reihenfolge.

In der Mengenlehre gibt es diverse weitere Arten von Objekten, die entweder als Container und/oder als Elemente auftreten können:

• Klassen sind Container: Sie können Elemente enthalten (und zwar Urelemente und Mengen).
• Urelemente können in Klassen als Elemente enthalten sein, können selbst aber keine Elemente enthalten. Typische Urelemente sind Zahlen, Zeichenketten, Boolesche Werte etc.
• Mengen sind spezielle Klassen (können also Elemente enthalten); sie können auch in Klassen als Elemente enthalten sein.
• Unmengen sind spezielle Klassen (können also Elemente enthalten); sie sind aber so umfangreich, dass sie nicht in irgendwelchen Klassen als Elemente enthalten sein können.

TO BE DONE

Glubrecht, Oberschelp, Todt: Individuen, reale und virtuelle Objekte

Zwischen Klassen und Klassenpaaren gibt es einen wichtigen Unterschied: Unmengen können keine Elemente von irgendwelchen Klassen sein, wohl aber (Paar-)Elemente von Klassenpaaren. Das heißt, mit Hilfe Klassenpaaren (und Klassentupeln) kann man auch Unmengen zu größeren Einheiten zusammenfassen. Mit Mengenpaaren geht dies nicht.

Allerdings gibt es nicht nur Mengen- und Klassenpaare. Ein geordnetes Paar kann – in speziellen formalen Systemen – an Stelle von Klassen und Urelementen auch andere Arten von Elementen enthalten. Gottlob Frege erlaubt beispielsweise „Gegenstände“, „Funktionen“ und „Werthverläufe“ als Elemente. John von Neumann erlaubt „Argumente“ (und damit insbesondere auch spezielle Funktionen, die sogenannten „Argument-Funktionen“) und in LISP sind nur Atome (Urelemente) und Paare als Elemente erlaubt.

Definitionen

Definition (Dipert (1982))

Definition von Randall Dipert, Dipert (1982), S. 354

An ordered pair is, roughly speaking, (a) an entity which contains two other entities and (b) is such that one of these two entities is identifiable as the 'first', the other as the 'second'. More precisely, the individuating criterion for ordered pairs is: two ordered pairs are identical just when their respective elements are identical. That ist, if $<A,B>$ and $<C,D>$ are ordered pairs with elements $A$, $B$, $C$, und $D$, then we wish to have:

$<A,B>=<C,D>$ if an only if $A=C$ and $B=D$.

Übersetzung (W. Kowarschick)
Ein geordnetes Paar ist, grob gesprochen, (a) eine Entität, die zwei andere Entitäten enthält und (b) zwar so, dass eine von diesen beiden Entitäten als die 'erste' identifiziert werden kann und die andere als die 'zweite'. Genauer gesagt, das individuierende Kriterium für geordnete Paare ist: zwei geordnete Paare sind genau dann identisch, wenn die entsprechenden Elemente identisch sind. Das heißt, wenn $<A,B>$ und $<C,D>$ geordnete Paare mit den Elementen $A$, $B$, $C$, und $D$ sind, dann möchten wir Folgendes haben:

$<A,B>=<C,D>$ genau dann, wenn $A=C$ und $B=D$.

Anmerkung (von Dipert)
No other property of ordered pairs has ever been shown to be necessary or desirable. This single property is sufficient.

Übersetzung (W. Kowarschick)
Von keiner anderen Eigenschaft geordneter Paare wurde jemals gezeigt, dass sie notwendig oder wünschenswert wäre. Diese eine Eigenschaft ist ausreichend.

Definition (Brockhaus (1991))

Brockhaus (1991): Band 16, S. 414

Paar [ahd. par ›zwei Dinge von gleicher Beschaffenheit‹, von lat. par ›gleich‹] Mathematik: eine Menge, die aus zwei Elementen (der ersten und der zweiten Komponente) besteht, die zusätzlich in einer Ordnung stehen: $(a,b)$ ist i. Allg. verschieden von $(b,a)$. P. lassen sich als Punkte im kartes. Produkt der zugrundeliegenden Menge mit sich selbst auffassen.

Definition (Kowarschick (2014))

Der Term $[a,b]$ heißt geordnetes Paar, wenn für den Operator $[\cdot ,\cdot ]$ das Paaraxiom erfüllt ist:

Zwei Paare $[a,b]$ und $[c,d]$ sind genau dann gleich, wenn sowohl $a$ und $c$ als auch $b$ und $d$ gleich sind.

$\bigwedge a,b:[a,b]=[c,d]\leftrightarrow a=c\wedge b=d$

Mengenpaare

Ein geordnetes Paar $[a,b]$ heißt Mengenpaar, wenn sowohl $a$ als auch $b$ eine Menge oder ein Urelement ist.

Klassenpaare

Ein geordnetes Paar $[a,b]$ heißt Klassenpaar, wenn sowohl $a$ als auch $b$ eine Menge, eine Unmenge oder ein Urelement ist. Insbesondere ist also jedes Mengenpaar ein Klassenpaar, aber die Umkehrung gilt nicht. Ein Klassenpaar, das wenigstens eine Unmenge enthält, ist kein Mengenpaar.

Anforderungen an den Paarbegriff

Dipert betont im Anschluss an seine Definition, dass das Paaraxiom zur Charakterisierung des Begriffs „geordnetes Paar“ ausreichend sei. Er ist der Meinung, dass von keiner anderen Eigenschaft geordneter Paare jemals gezeigt wurde, dass sie notwendig oder zumindest wünschenswert wäre.

Glubrecht, Oberschelp und Todt stellen die noch allgemeinere Forderung auf, dass die Definition des Paarbegriffs „adäquat“ sein müsse (Glubrecht, Oberschelp, Todt (1983), S. 203). Darunter verstehen sie, dass nicht nur das Paaraxiom erfüllt sein muss, sondern dass, falls Paare klassentheoretisch definiert werden, Paare von „ realen Objekten“ stets auch selbst „reale Objekte“ sind. Die Unterscheidung zwischen realen und virtuellen Objekten wurde zur Vermeidung von Antinomien wie der Russellschen Antinomie eingeführt. Sie geht auf Quine (1963) zurück.

Da reale Objekte gemäß ihrer Definition Elemente von anderen Objekten sein können, hat die Forderung von Glubrecht, Oberschelp und Todt zur Folge, dass Paare von realen Objekten ebenfalls Elemente anderer Objekte sein können. Dies ist für klassentheoretische Systeme sicherlich eine zumindest „wünschenswerte“ Zusatzforderung. Ob dagegen Paare von virtuellen Objekten überhaupt definiert werden können und falls „ja“, ob diese dann auch Elemente von anderen Objekten sein können, steht zunächst noch auf einem ganz anderen Blatt.

Schmidt hatte bereits 1966 gefordert, dass Paare nicht nur für Mengen (reale Objekte), sondern auch für Unmengen (echte Klassen, virtuelle Objekte) definiert sein müssen.

Zusammenfassend ergeben sich also folgende notwendigen bzw. wünschenswerte Forderungen, die eine formale Definition von geordneten Paaren erfüllen muss bzw. sollte:

1. Das Paaraxiom muss erfüllt sein.
2. Möglichst viele, am Besten natürlich alle Objekte des zugrundeliegenden Universiums sollten als Paarelemente erlaubt sein. Insbesondere sollten Paare selbst Elemente von Paaren sein können.
3. Der Paarbegriff sollte problemlos zum Begriff des n-Tupels verallgemeinert werden können. Dies ist ganz einfach möglich, falls Paare Elemente von Paaren sein können, falls also die vorangegangene Forderung erfüllt wird.
4. Möglichst viele Paare sollten in Containern wie Mengen, Klassen etc. zusammengefasst werden können. Wünschenswert wäre sicherlich, dass auch diese Forderung von allen Paaren erfüllt werden würde. Das ist aber aufgrund von Antinomien, die sich daraus i. Allg. ergeben würden, ein unrealistischer Wunsch.

Projektionsoperatoren

Für geordnete Paare gibt es – wegen des Paaraxioms – zwei Projektionsoperatoren ${\pi }_1$ und ${\pi }_2$, die das erste bzw. das zweite Element des Paars extrahieren. Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich normalerweise nicht um Funktionen, da der Funktionsbegriff überlicherweise erst nachträglich mit Hilfe des Paarbegriffs definiert wird. Es handelt sich häufig um abkürzende Schreibweisen, die durch die sie definierenden Terme ersetzt werden können. Daher werden ${\pi }_1$ und ${\pi }_2$ hier Operatoren genannt.

Definition (Kowarschick (2014))

Operatoren ${\pi }_1$ und ${\pi }_2$, die das erste bzw. das zweite Element eines jeden Paars (des zugehörigen Universums) extrahieren, heißen Projektionsoperatoren:

$\bigwedge a,b:{\pi }_1([a,b])=a$ (das erste Element des jeweiligen Paars)

$\bigwedge a,b:{\pi }_2([a,b])=b$ (das zweite Element des jeweiligen Paars)

Anmerkung

Die hier verwendeten Bezeichnungen ${\pi }_1$ und ${\pi }_2$ für die Projektionsoperatoren gehen auf Edgar Codd zurück, den Begründer der Relationalen Algebra.

Außerhalb der Datenbankwelt haben sich für diese Operatoren noch keine Standardbezeichnungen durchgesetzt. Daher gibt es in der Literatur ganz unterschiedliche Namen, wie man an folgender kleinen, aber sicher unvollständigen Liste erkennt:

• Rosser (1953): $Q_1$ und $Q_2$
• McCarthy (1960): car und cdr
• Morse (1965): ${\mathrm{c}\mathrm{r}\mathrm{d}}^{\prime }$ und ${\mathrm{c}\mathrm{r}\mathrm{d}}^{″}$
• Schmidt (1966): $\mathfrak{G}$ und ${\mathfrak{G}}^{\prime }$
• Ebbinghaus (2003): ${\pi }_l$ und ${\pi }_r$

Eigenschaften der Projektionsoperatoren

Da die Projektionsoperatoren zuvor nur metasprachlich definiert wurden, kann man Eigenschaften von ${\pi }_1$ und ${\pi }_2$ zunächst auch nur auf Metaebene beweisen. Sobald man den Paarbegriff objektsprachlich formalisiert hat (siehe nachfolgende Beispiele), kann man analoge Aussagen mit Hilfe der zugehörigen Objektsprache beweisen. Und wenn einem eine objektsprachliche Formalisierung des Funktionsbegriffs zur Verfügung steht, kann man auch Projektionsfunktionen definieren.

Existenz und Eindeutigkeit der Projektionsoperatoren

Wenn das Paaraxiom erfüllt ist und alle Paare $p$ in der Form $[a,b]$ dargestellt werden können, gibt es genau einen Operator ${\pi }_1$ und genau einen Operator ${\pi }_2$ mit folgenden Eigenschaften:

• ${\pi }_1$ und ${\pi }_2$ sind nur für Paare definiert
• ${\pi }_1([a,b])=a$
• ${\pi }_2([a,b])=b$

Insbesondere gilt damit für jedes Paar $p$ die Beziehung $p=[{\pi }_1(p),{\pi }_2(p)]$.

Beweis

siehe Satz „Existenz und Eindeutigkeit der Projektionsoperatoren“

Anmerkung

Der Satz sagt nicht aus, dass es nicht zwei unterschiedliche Projektionsoperatoren ${\pi }_1^{\prime }$ und ${\pi }_1^{″}$ bzw. ${\pi }_2^{\prime }$ und ${\pi }_2^{″}$ geben kann, die zusätzlich auch für Nicht-Paare $\bar{p}$ definiert sind und für derartige Elemente evtl. unterschiedliche Ergebnisse liefern:

${\pi }_1^{\prime }(\bar{p})\ne {\pi }_1^{″}(\bar{p})$ bzw. ${\pi }_2^{\prime }(\bar{p})\ne {\pi }_2^{″}(\bar{p})$

Für jedes Paar $p=[a,b]$ gilt aber stets ${\pi }_1^{\prime }(p)={\pi }_1^{″}(p)=a$ und ${\pi }_2^{\prime }(p)={\pi }_2^{″}(p)=b$.

Aus der Existenz der Projektionsoperatoren folgt das Paaraxiom

Wenn zwei Projektionsoperatoren ${\pi }_1$ und ${\pi }_2$ existieren, die für alle Paare $[a,b]$ die Bedingungen

• ${\pi }_1([a,b])=a$
• ${\pi }_2([a,b])=b$

erfüllen, dann ist auch das Paaraxiom erfüllt.

Beweis

siehe Satz „Aus der Existenz der Projektionsoperatoren folgt das Paaraxiom“

Anmerkung

Dieser Satz ist die Umkehrung des vorangegangen Satzes. Außerdem folgt aus dem vorangegangen Satz sofort, dass zwei Projektionsoperatoren, wenn sie auf das „Universum“ aller Paare eingeschränkt werden, eindeutig sind, sofern sie überhaupt existieren.

Geschichte des Paarbegriffs

TO BE DONE

Paaraxiom von Hamilton, Hamilton (1837), S. 300 und nachfolgende Geschichte

Peirce (1870), S. 359

Der Mathematiker und Philosoph Charles Sanders Peirce merkt 1870 als Erster an, dass eine Relation (die bei Peirce “relative” heißt) als Klasse von “elementary relatives” aufgefasst werden kann, wobei er unter “elementary relatives” Beziehungen zwischen Paaren, Tripletts, Quartetten etc. von Individuen versteht. Die Bedeutung der Begriffe „Paar“, „Triplett“, „Quartett“ etc. setzt er dabei allerdings als bekannt voraus.

Erste Definition des geordneten Paares, Peano (1889), S. XII6

Die symbolische Schreibweise $(x,y)$ für geordnete Paare verwendet Giuseppe Peano erstmals in der 1889 erschienen Arbeit „Arithmetices principia: nova methodo“:

Sint $x$, $y$ entia quaecumque; systema ex ente $x$ et ex ente $y$ compositum ut novum ens consideramus, et signo $(x,y)$ indicamus;

Übersetzung (W. Kowarschick)

Es seien $x$, $y$ beliebige Entitäten; das System, das aus Entität $x$ und aus Entität $y$ zusammengesetzt ist, fassen wir als neue Entität auf und bezeichnen es mit dem Zeichen $(x,y)$;

Allerdings hat Peano in dieser bahnbrechenden Arbeit – hier wurden erstmals die so genannten Peano-Axiome zur Definition der Natürlichen Zahlen formuliert – weder das Paaraxiom noch den eigentlichen Begriff „Paar“ eingeführt.

Im Jahr 1893 definiert Gottlob Frege geordnete Paare funktional mit Hilfe der von ihm zuvor eingeführten Element- und „Werthverlauf“-Operatoren – also mit Hilfe anderer „Grundbegriffe“ – und beweist diejenigen Eigenschaften, die das – vier Jahre später von Peano formulierte – Paaraxiom für den Paarbegriff fordert (siehe Abschnitt Frege (1893)). Allerdings blieb die Wirkung von Frege gering, „auch wegen seiner Verwendung zahlreicher und ungewöhnlicher Symbole“, wie Wußing in seiner „kulturhistorischen Zeitreise“ anmerkt. Es dauert 38 Jahre, bis Alonzo Church 1941 im Rahmen des Lamda-Kalküls abermals eine funktionale Definition des Paarbegriffs vorschlägt. Diese unterschiedet sich im Prinzip nicht von Freges Definition (siehe Geordnetes Paar: Definition von Frege).

Definition des geordneten Paars und Paaraxiom, Peano (1897b), S. 6

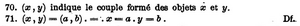
In zwei Veröffentlichungen von 1897 formuliert Giuseppe Peano erstmals das Paaraxiom.

70. $(x,y)$ indique le couple formé des objets $x$ et $y$.
71. $(x,y)=(a,b).=.x=a.y=b$.

Übersetzung (W. Kowarschick)

70. $(x,y)$ bezeichnet das Paar gebildet aus den Objekten $x$ und $y$.
71. $\bigwedge x,y,a,b:(x,y)=(a,b)\leftrightarrow x=a\wedge y=b$.

Außerdem führt er aus, dass die Idee eines geordneten Zahlenpaars von grundsätzlicher Bedeutung sei, er aber nicht wisse, wie er es durch die von ihm zuvor definierten Symbole ausdrücken könne. Ihm war also bereits bewusst, dass es vorteilhaft wäre, wenn man den Paarbegriff auf andere Grundbegriffe zurückführen könnte. (Im selben Aufsatz führt Peano übrigens kurz nach dem Paaraxiom auch noch den Existenzoperator $\mathrm{\exists }$ als zweite bedeutende Neuerung ein.)

Dreizehn Jahre später veröffentlichen Alfred North Whitehead und Bertrand Russell den ersten Band der Principia Mathematica. Ihr Ziel war es, „die Mathematik vollständig auf eine formal-logische Grundlage zu stellen“. (Der Versuch musste allerdings fehlschlagen, wie Kurt Gödel 1931 eindrucksvoll bewies.) In diesem ersten Band versuchen die beiden Autoren, die von Russell entdeckte Anitomie zu vermeiden, indem sie für Mengen, Relationen und Funktionen spezielle Typhierarchien einführen. Da sie zu dieser Zeit noch nicht wissen, wie man Relationen und Funktionen auf Mengen zurückführen kann, bleibt ihnen nichts weiter übrig, als alle drei Grundbegriffe der Mathematik separat zu behandeln. Geordnete Paare definieren sie im Anschluss an diese Grundbegriffe mit Hilfe des kartesischen Produktes von einelementigen Mengen.

1914 gelingt es Felix Hausdorff und Norbert Wiener unabhängig voneinander, erstmals geordnete (Mengen-)Paare durch Mengen auszudrücken. Damit war es möglich, den Begriff „Relation“ und damit insbesondere auch den Begriff „Funktion“ (da Funktionen spezielle Relationen sind) auf den Mengenbegriff zurückzuführen. Eine Relation kann – wie von Peirce bereits 1870 erkannt wurde (siehe oben) – als Menge bzw. Klasse von Paaren oder – allgemeiner – von Tupeln aufgefasst werden. Das heißt, man konnte von 1914 an auf spezielle Typisierung von und spezielle Axiome für Relationen und Funktionen verzichten. Nun definierte man das kartesische Produkt mit Hilfe von geordneten Paaren und nicht umgekehrt, wie es noch Russell und Whitehead getan hatten.

Sieben Jahre später findet Kazimierez Kuratowski eine Definition, die einfacher ist als Wieners Definition und im Gegenstatz zu Huasdorffs Definition ohne Spezialelemente auskommt. Heute findet man oftmals Autoren, die von „Wiener-Paaren“ sprechen, aber „Kuratowki-Paare“ meinen.

Die Weiterentwicklung des Paarbegriffs

Wenn man irgendeinen Grundbegriff mit Hilfe anderer Grundbegriffe definiert, dann hat der so definierte Grundbegriff zusätzliche Eigenschaften. Wenn man beispielsweise die Ordinalzahlen auf die von John von Neumann vorgeschlagene Weise definiert, gilt für alle Ordinalzahlen $m$ und $n$:

$m<n\leftrightarrow m\in n$

Diese Eigenschaft hat sich als vorteilhaft erwiesen, gilt aber nicht im Axiomensystem der natürlichen Zahlen von Peano, da dort der Elementoperator für natürliche Zahlen gar nicht definiert ist. Dass alle Hausdorff-Paare $[a,b]$ folgende Eigenschaft haben,

$\{\mathbf{1},\mathbf{2}\}\subseteq \bigcup [a,b]$

ist dagegen eher nachteilig.

Man benötigt allerdings keine dieser beiden hier beispielshaft aufgeführten Zusatzeigenschaften wirklich, um wesentliche Eigenschaften von natürlichen Zahlen bzw. geordneten Paaren zu zeigen.

Vorschlag für ein Klassenpaar, Quine (1981), S. 202, erstmals 1940 publiziert

Eine negative Eigenschaft der Kuratowski-Paare beschäftigt Willard Quine Ende der 30er-Jahre und in den 40er-Jahren. Wenn man der Mengenlehre eine Typhierarchie zugrunde legt, liegt ein Kuratowski-Paar um mindestens zwei Ebenen höher als jedes seiner beiden Elemente. (Das gilt auch für Hausdorff-Paare. Wiener-Paare liegen sogar mindestens drei Ebenen höher.) Gerade bei einer reinen, d. h. nicht-kumulativen Typhierachie ist dies lästig. Aber auch bei der von Quine im Jahre 1937 vorgeschlagenen Art der Typisierung ist dies sehr unpraktisch.

Goodmans Anmerkung zu Quines Klassenpaar-Definitionen, Goodman (1941), S. 150

Eine weiteres Problem der Kuratowski-Paare ist, dass sie nur Mengen, aber keine Unmengen als Paarelemente enthalten können. Quine verwendet in seinem Lehrbuch „Mathematical Logic“ von 1940 zwar noch die Kuratowski-Paare, gibt aber bereits eine alternative Paar-Definition an, bei der geordnete Paare auch Unmengen enthalten können. Allerdings erkennt er bald, dass diese Definition fehlerhaft ist, und diskutiert mit Nelson Goodman über dieses Problem:

[...] Quine suggested an alternative to the definition of ordered couple [...], but later discovered that this alternative definition would fail to distinguish $x,y$ from $y,x$ when $x\subset y$. In a later discussion between us he proposed the first satisfactory definition of the ordered couple as a class only one type higher than its components.

Übersetzung (W. Kowarschick)

[...] Quine schlug eine Alternative für die Definition von geordneten Paaren vor [...], bemerkte aber später, dass diese Alternative daran scheitert $x,y$ und $y,x$ zu unterscheiden, wenn $x\subset y$. In einer späteren Diskussion zwischen uns schlug er die erste zufriedenstellende Definition des geordneten Paares als eine Klasse vor, die nur eine Ebene höher liegt, als seine Komponenten.

Goodman merkt jedoch kritisch an, dass diese Definition nicht problemlos verallgemeinert werden kann, um „längere Sequenzen“ (d. h. $n$-Tupel mit $n>2$) zu definieren. Er verbessert daher Quines Definition so, dass – erstens – ein Paar weiterhin nur um eine Ebene höher liegt als seine Elemente und – zweitens – diese Definition problemlos für $n$-Tupel verallgemeinert werden kann.

Dies wiederum stachelt Quine an, Goodmans Definition zu verbessern. 1945 präsentiert er eine Paardefinition, bei der jedes Paar auf derselben Ebene liegt wie ihre Elemente und die für beliebige $n$-Tupel verallgemeinert werden kann. Diese $n$-Tupel liegen dann ebenfalls auf derselben Ebene wie ihre Elemente.

Quines primäres Ziel war es, eine Paardefinition anzugeben, die sich bezüglich der von ihm definierten Typhierarchie „gutartig“ verhält. Seine Idee, nicht die Paarelemente selbst, sondern deren Elemente zur Definition des zugehörigen Paares zu verwenden, hatte aber noch einen ganz anderen Vorteil. Auf diese Weise war es möglich, nicht nur Mengenpaare, sondern sogar Klassenpaare zu definieren. Mehrere Mathematiker, wie z. B. Morse (1965) oder Schmidt (1966) griffen diese Idee auf, und definierten auf diese Weise explizit Klassenpaare.

Ein Nachteil der Idee von Quine ist, dass Urelemente keine Klassen sind und damit keine Elemente enthalten. Das heißt, seine Definition sowie die Definitionen vom Morse, Schmidt und anderen funktionieren nur in Klassenuniversen, in denen es keine Urlemente gibt. Diese Bedingung ist allerdings in den Klassensystemen, die die Autoren verwenden, jeweils erfüllt. Mit Hilfe der leeren Menge und ein paar Mengenbildungsaxiomen lassen sich beliebig viele Mengen erzeugen, die als Repräsentanten für die fehlenden Urelemente dienen können.

1967 schlägt Martin Kühnrich erstmals Klassenpaar-Definitionen vor, die auch für Klassenuniversen mit Urelementen korrekt ist. Im Jahr 1981 geben Arnold Oberschelp und Günter Todt eine Klassenpaar-Definition an, die sogar in Klassenuniversen mit Urelementen und weiteren unspezifischen Objekten korrekt ist. Außerdem wird für den Beweis der „Adäquatheit“ der Definition, d. h. für den Nachweis, dass das Paaraxiom erfüllt ist und dass Paare von Mengen selbst Mengen sind, nur das Paarmengenaxiom benötigt.

Bedeutung des Paarbegriffs

Der Paarbegriff ein ganz fundamentales Werkzeug der Mathematik und der Informatik und steht in dieser Hinsicht der Zahl 0 oder der leeren Menge in keiner Hinsicht nach.

Im Jahr 2003 verfasste Akihiro Kanamori einen sehr schönen Übersichtsartikel über die Geschichte dreier für ihn fundamentaler Begriffe der Mengenlehre. Für ihn sind dies die Begriffe „leere Menge“, „einelementige Menge“ und „geordnetes Paar“:

For the modern set theorist the empty set $0$, the singleton $\{a\}$, and the ordered pair $<x,y>$ are at the beginning of the systematic, axiomatic development of set theory, both as a field of mathematics and as a unifying framework for ongoing mathematics. These notions are the simplest building blocks in the abstract, generative conception of sets advanced by the initial axiomatization of Ernst Zermelo [l908a] [...]

Für moderne Mengentheoretiker sind die leere Menge $0$, die einelementige Menge $\{a\}$ und das geordnete Paar $<x,y>$ der Anfang der systematischen, axiomatischen Entwicklung der Mengenlehre, sowohl als [eigenständiges] Gebiet der Mathematik, als auch als vereinendes Grundgerüst für die aktuelle Mathematik. Diese Begriffe sind die einfachsten Bausteine des abstrakten, generativen Konzepts der Mengen angereichert durch die initiale Axiomatisierung von Ernst Zermelo [l908a] [...] (Übersetzung des vorangegangen Absatzes)

Gut zwanzig Jahre vorher hatte schon Randall Dipert, C.S. Peirce Professor of American Philosophy, die Bedeutung des geordneten Paars für die präzise Definition des Relations- und des Funktionsbegriffs betont, die für ihn „unabdingbar für das Verständnis der Fundamente der Mathematik sind“:

One of the most significant discoveries of early twentieth century mathematical logic was a workable definition of ´ordered pair´ totally within set theory. [...] A definition of ´ordered pair´ held the key to the precise formulation of the notions of ´relation´ and ´function´ – both of which are probably indispensable for an understanding of the foundations of mathematics. The set-theoretic definition of 'ordered pair' thus turned out to be a key victory for logicism, providing one admits set theory is logic.

Eine der bedeutsamsten Entdeckungen des frühen zwanzigsten Jahrhunderts [auf dem Gebiet der] mathematischen Logik war eine funktionsfähige Definition des ´geordneten Paars´ vollkommen innerhalb der Mengenlehre. [...] Eine Definition des ´geordneten Paars´ war der Schlüssel zur präzisen Formulierung der Begriffe ´Relation´ und ´Funktion´ – welche beide vermutlich unabdingbar für das Verständnis der Fundamente der Mathematik sind. Die mengentheoretische Definition des ´geordneten Paars´ erwies sich folglich als Schlüsselerfolg für den Logizismus, vorausgesetzt, man erkennt an, dass Mengenlehre Logik ist. (Übersetzung des vorangegangen Absatzes)

Allerdings geht es Dipert nicht so sehr um das geordnete Paar an sich, sondern um die Darstellung des geordneten Paars mit Hilfe von ungeordneten Mengen. In seinem Aufsatz möchte er aufzeigen, „wie inadäquat die mengentheoretischen Untersuchungen und Erklärungen von so wichtigen Begriffen wie Relation und Funktion sind“.

I shall attempt to show that the development of a set-theoretic notion of ordered pair was in fact only a pyrrhic victory for logicism, and that all popular, and even all possible, set-theoretic definitions of ´ordered pair´ are flawed. This fact in turn will show how inadequate have been set-theoretic analyses and explications of such important notions as relation and function. I conclude by pointing out that the only philosophically viable route appears to be the approach advocated by Schröder and Peirce a century ago.

Ich werde versuchen zu zeigen, dass die Entwicklung eines mengentheoretischen Begriffs des geordneten Paares tatsächlich nur ein Pyrrhussieg für den Logizismus war und dass alle populären, eventuell sogar alle möglichen mengentheoretischen Definitionen des ´geordneten Paars´ mit Makeln behaftet sind. Diese Tatsache zeigt wiederum, wie inadäquat die mengentheoretischen Untersuchungen und Erklärungen von so wichtigen Begriffen wie Relation und Funktion sind. Ich schließe, indem ich aufzeige, dass der einzig philosophisch gangbare Weg anscheinend der Ansatz ist, den Schröder und Peirce vor einem Jahrhundert verfochten haben. (Übersetzung des vorangegangen Absatzes)

Dieser Kritik an der mengentheoretischen Definition des geordnenten Paares muss deutlich wiedersprochen werden. Aus mathematischer Sicht dient die Reduktion von Grundbegriffen und Axiomen immer nur der Vereinfachung, d. h. der Arbeitserleichterung. Es spricht ansonsten überhaupt nichts dagegen, einen anderen Weg zu gehen:

• Es ist nicht notwendig, Paare als spezielle Mengen aufzufassen. Dies ist nur eine Möglichkeit, Paare auf andere Grundbegriffe zurückzuführen. Diverse andere Möglichkeiten werden im nachfolgenden Abschnitt Integration von geordneten Paaren in formale Systeme aufgezeigt.
• Es ist noch nicht einmal notwendig, den Paarbegriff auf andere Grundbegriffe zurückzuführen. Der Paarbegriff kann und wird in der Mathematik und in der Informatik durchaus auch axiomatisch eingeführt, wie im Abschnitt Axiomatische Definition von geordneten Paaren gezeigt wird.
• Verschiedenen Grundbegriffen, wie „Menge“, „geordnetes Paar“/„Tupel“, „Funktion“, „Relation“ etc., können unterschiedliche „Universen“ zugeordnet werden, wie es z. B. Whitehead und Russell in der Principia Mathematica praktiziert haben.. Diese Vorgehensweise ist in der Informatik sogar noch weiter verbreitet als in der Mathematik. Jede Programmierprache unterscheidet mehr oder weniger scharf zwischen atomaren Typen, Containertypen (Mengen, Multimengen, Listen etc.), Funktionen und weiteren Datentypen.

Dipert hat recht, wenn er aus philosophischer Sicht eine Trennung der verschiedenen Begriffe für wesentlich hält. Dies steht jedoch überhaupt nicht im Widerspruch zur mathematischen Vorgehensweise, aus Vereinfachungsgründen einen Begriff auf einen anderen zurückzuführen. Man muss dann nur sauber unterscheiden zwischen Aussagen, die innerhalb einer speziellen Theorie gültig sind, und Aussagen, die in jeder Theorie gültig sind, die bestimmte Grundbegriffe wie „geordnete Paare“, „Funktionen“, „Relationen“, „Ordinalzahlen“ etc. in Übereinstimmung mit den üblichen Bedeutungen definiert. Beispielsweise gilt die Aussage $m<n\leftrightarrow m\in n$ nur für Ordinalzahlen, die auf die von John von Neumann vorgeschlagene Weise mit Hilfe von Mengen definiert wurden, hingegen gilt die Aussage $n\ne 0\to 0<n$ für alle Ordinalzahlen, unabhängig davon, wie die Ordinalzahlen definiert wurden, solange nur die Null und die Kleinerrelation die übliche Bedeutungen haben.

Integration von geordneten Paaren in formale Systeme

Um geordnete Paare in ein formales System wie ein Mengensystem, ein Klassensystem, eine Programmiersprache oder Ähnliches zu integrieren, gibt es mehrere Möglichkeiten. Die wichtigsten dieser Möglichkeiten sind die funktionale, die relationale, die mengentheoretische, die klassentheoretische und, last, but no least, die axiomatische Definition des Paarbegriffs.

Funktionale Definition von geordneten Paaren

In einem formalen System, in dem Funktionen Basiselemente sind, können geordnete Paare mit Hilfe von (Lambda-)Funktionen definiert werden.

Beispiele

	Notation	Definition	GlossarWiki-Definition
Frege (1893)	$a;b$	$⊩\acute{ϵ}(a⌢(b⌢ϵ))=a;b$	$[a,b{]}_F:=\lambda x.xba(=\lambda ϵ.ϵba)$ (vgl. Artikel „Geordnetes Paar: Definition von Frege“)
Church (1941) (Lambda-Kalkül)	$[a,b]$	$[a,b]\to \lambda x.xab$	$[a,b{]}_C:=\lambda x.xab$

Erstaunlicherweise liegt den beiden Definitionen von Frege und Church, zwischen deren Veröffentlichungen mehrere Jahrzehnte liegen, dieselbe Idee zugrunde. Ob sich Church an Freges Definition orientiert hat, ist allerdings unklar.

In beiden Fällen wird ein geordnetes Paar durch eine Funktion ausgedrückt, die eine „Extraktionsfunktion“ als Argument für den Parameter $x$ (bzw. $ϵ$) erwartet. Dieser Funktion werden $a$ und $b$ nacheinander als Argumente übergeben. Sie hat die Aufgabe, entweder $a$ oder $b$ als Ergbnis zu liefern, je nachdem, ob das erste oder das zweite Element des Paares extrahiert werden soll:

$\lambda x.\lambda y.y$ (Extraktionsfunktion für das erste Element eines Fregepaars bzw. das zweite Element eines Churchpaares)

$\lambda x.\lambda y.x$ (Extraktionsfunktion für das zweite Element eines Fregepaars bzw. das erste Elemet eines Churchpaares)

Die eigentlichen Projektionsfunktionen übergeben dem aktuellen geordneten Paar $p$ die entsprechende Extraktionsfunktion zur Auswertung. Beispielsweise sind die Projektionsfunktionen für Fregepaare $\lambda x.xba$ folgendermaßen definiert:

$\begin{array}{lcl}{\pi }_1& :=& \lambda p.p(\lambda x.\lambda y.y)\\ {\pi }_2& :=& \lambda p.p(\lambda x.\lambda y.x)\end{array}$

$\begin{array}{lclclclll}{\pi }_1(\lambda x.xba)& =& (\lambda x.xba)(\lambda x.\lambda y.y)& =& (\lambda x.\lambda y.y)ba& =& (\lambda y.y)a& =& a\\ {\pi }_2(\lambda x.xba)& =& (\lambda x.xba)(\lambda x.\lambda y.x)& =& (\lambda x.\lambda y.x)ba& =& (\lambda y.b)a& =& b\end{array}$

Relationale Definition von geordneten Paaren

In Systemen, in denen Relationen Basiselemente sind, können geordnete Paare als spezielle Relationen definiert werden.

Beispiele

	Notation	Definition	GlossarWiki-Definition
Whitehead, Russell (1910)	$(x,y)$	... an ordinal couple (geordnetes Paar) ... is defined as a relation $\iota ‘x\uparrow \iota ‘y$ ...	$[x,y{]}_{WR}:=\{x\}\times \{y\}$

Whitehead und Russell bezeichnen das kartesische Produkt zweier Mengen $a$ und $b$ mit $a\uparrow b$ und die einelementige Menge, die $x$ als einziges Element enthält, mit $\iota ‘x$. Sie führen zuerst den Begriff „Relation“ axiomatisch ein, definieren darauf aufbauend das „kartesisches Produkt“ (wenn auch nicht unter diesem Namen) und darauf aufbauend den Begriff „geordnetes Paar“. In mengen- oder klassenbasierten Systemen (siehe nachfolgende Abschnitte) geht man genau umgekehrt vor.

Mengentheoretische Definition von geordneten Paaren

In einem formalen System, in dem Mengen als Basiselemente existieren, können geordnete Paare als spezielle Mengen definiert werden.

Beispiele

	Notation	Definition	GlossarWiki-Definition
Hausdorff (1914)	$(a,b)$	$\{\{a,1\},\{b,2\}\}$	$[a,b{]}_H:=\{\{a,1\},\{b,2\}\}$
Wiener (1914)	kein spezieller Term	$\iota ‘(\iota ‘\iota ‘x\cup \iota ‘\mathrm{\Lambda })\cup \iota ‘\iota ‘\iota ‘y$	$[x,y{]}_W:=\{\{\{x\},\mathrm{\varnothing }\},\{\{y\}\}\}$
Kuratowski (1921)	kein spezieller Term	La classe $((a,b),(a))$ est une „paire ordonnée dont $a$ est le premier élément et $b$ est le second“	$[a,b{]}_K:=\{\{a,b\},\{a\}\}$
Quine (1940)	$x;y$	$\iota (\iota x\cup \iota \mathrm{\Lambda })\cup \iota \iota y$	$[x,y{]}_{Q40}:=\{\{x,\mathrm{\varnothing }\},\{y\}\}$
Quine (1986)	$⟨x,y⟩$	$⟨x,y⟩$: the set whose two members are $\{\{a\},1\}$ and $\{\{b\},2\}$	$[x,y{]}_{Q86}:=\{\{\{a\},1\},\{\{b\},2\}\}$

Da Mengen ungeordnet sind, d. h. die Elemente keine bestimmte Reihenfolge haben, muss man das erste und das zweite Element eines geordneten Paares anderweitig unterscheiden. Eine Möglichkeit ist es, für jedes Paarelement dessen Position im Paar explizit anzugeben. Diesen Weg schlagen Hausdorff und Quine (1986) ein. Eine andere Möglichkeit ist es, die Reihenfolge der Paarelemente mit Hilfe der Mächtigkeit von Mengen eindeutig festzulegen. Die Definitionen von Wiener, Kuratowski und Quine (1940) basieren allesamt auf der Idee, die Paarlemente anhand einer ein- und einer zweielementigen Menge zu unterscheiden.

Klassentheoretische Definition von geordneten Paaren

In einem formalen System, in dem es neben Mengen auch noch Unmengen gibt, d. h., in dem es Klassen gibt, die nicht Element einer anderen Klasse sein können, können die Mengenpaar-Definitionen von Hausdorff, Wiener, Kurtowski, Quine etc. nicht verwendet werden. In allen diesen Definitionen werden die Paarelemente selbst als Elemente in spezielle Klassen eingefügt.

1940 hatte Quine die Idee, nicht die Paarelemente selbst, sondern die Elemente dieser Klassen zu verwenden, um Paare zu definieren. Jedes Element einer Klasse ist automatisch eine Menge und kann daher auch Element einer anderen Klasse sein, z. B. einer Klasse, die ein geordnetes Paar definiert. Allerdings war Quines Definition von 1940 noch fehlerhaft, wie er selbst kurz drauf feststellen musste.

Ein Nachteil der Idee von Quine ist, dass Urelemente keine Klassen sind und damit keine Elemente enthalten. Das heißt, die im Folgenden aufgelisteten Klassenpaar-Definitionen funktioneren im Gegensatz zu den Mengenpaar-Definitionen des vorangegangen Abschnitts nur in Klassenuniversen, in denen es keine Urlemente gibt. Diese Bedingung ist heute allerdings meist erfüllt. Mit Hilfe der leeren Menge und ein paar Mengenbildungsaxiomen lassen sich beliebig viele Mengen erzeugen, die als Repräsentanten für die fehlenden Urelemente dienen können.

Beispiel 1

	Notation	Definition	GlossarWiki-Definition
Quine (1945)	$x;y$	$\begin{array}{rllll}\theta z& =& \hat{u}(\mathrm{\exists }v)& (& v\in z:\\ & & & & \sim v\in Nn.u=v\\ & & & & .\vee .\\ & & & & v\in Nn.u=Sv\\ & & & )\\ \\ x;y& =& \hat{w}(\mathrm{\exists }z)& (& \\ & & & & z\in x.w=\theta z\\ & & & & .\vee .\\ & & & & z\in y.w=\theta z\cup \iota 0\\ & & & )\end{array}$	$\begin{array}{rllll}\theta (z)& :=& \{u|\bigvee v\in z:& & \\ & & (v\notin \mathbb{N}\wedge u=v)\\ & & \vee \\ & & (v\in \mathbb{N}\wedge u=v+1)\\ & & \}\\ \\ [x,y{]}_{Q45}& :=& \{w|\bigvee z:& \\ & & (z\in x\wedge w=\theta (z))\\ & & \vee \\ & & (z\in y\wedge w=\theta (z)\cup \{0\})\\ & & \}\end{array}$

Quine definiert einen Operator $\theta$, der jede Klasse $z$ auf eine neue Klasse $\theta (z)$ abbildet, die im Wesentlichen dieselben Elemente wie $z$ enthält. Allerdings wird jede natürliche Zahl, die in $z$ enthalten ist, um $1$ erhöht. Der Operator $\theta$ hat zwei Eigenschaften: Zum einen enthält $\theta (z)$ mit Sicherheit nicht die natürliche Zahl $0$, da $0$ nicht der Nachfolger irgendeiner natürlichen Zahl ist, und zum anderen kann $z$ aus $\theta (z)$ sowie aus $\theta (z)\cup \{0\}$ zurückgewonnen werden, indem die Zahl $0$ gegebenenfalls entfernt wird und jede andere natürliche Zahl, die in $\theta (z)$ enthalten ist, um $1$ verringert wird.

Das Paar $x;y$ definiert Quine nun einfach als Vereinigung zweier Klassen. Die erste Klasse enthält für jedes Element $z$ von $x$ das Element $\theta (z)$ und die zweite Klasse enthält für jedes Element $z$ von $y$ das Element $\theta (z)\cup \{0\}$. (Dass $\theta (z)$ nicht nur für Mengen, sondern sogar für Klassen definiert ist, ist hier nicht von Bedeutung, da jedes Element einer beliebigen Klasse stets eine Menge ist.) Da $\theta (z)$ nie die Null als Element enthält, kann für jedes Element der Paarklasse $x;y$ eindeutig entschieden werden, ob es zum ersten Element $x$ oder zum zweiten Element $y$ gehört.

Beispiel 2

	Notation	Definition	GlossarWiki-Definition
Morse (1965)	$(a,b)$	$\begin{array}{rcl}((x{}_{´}y)& \equiv & \{\{x\},\{x,y\}\})\\ {a{}_{´}}_{´}b& \text{ist}& \text{zugeh}\ddot{\text{o}}\text{riges kartesisches Produkt}\\ (\text{ss}a& \equiv & (\text{sng}0\cup \bigvee x(x\in a\wedge \text{sng}\text{sng}a)))\\ ((a,b)& \equiv & ((\text{sng}{0{}_{´}}_{´}\text{ss}a)\cup (\text{sng}\text{sng}{0{}_{´}}_{´}\text{ss}b)))\end{array}$	$\begin{array}{rcl}[a,b{]}_K& :=& \{\{x\},\{x,y\}\}\\ a{\times }_{K}b& :=& \{[x,y{]}_K|x\in a,y\in b\}\\ s(a)& :=& \{\mathrm{\varnothing }\}\cup \{\{x\}|x\in a\}\\ [a,b{]}_M& :=& (\{\mathrm{\varnothing }\}{\times }_{K}s(a))\cup (\{\{\mathrm{\varnothing }\}\}{\times }_{K}s(b))\end{array}$

Morse schlägt einen anderen Weg ein. Er definiert zunächst Mengenpaare $(x{}_{´}y)$ und das zugehörige kartesische Produkt auf die von Kuratowski vorgeschlagene Weise. Der Operator ${}_{´}$ liefert nur für Mengen sinnvolle Ergebnisse, das zugehörige kartesische Produkt ${a{}_{´}}_{´}b$ ist dagegen auch für Klassen definiert. In einem zweiten Schritt definiert Morse einen Operator $ss$, der jedes Element $x$ einer Klasse $a$ durch die einelementige Klasse $\{x\}$ ersetzt. Außerdem fügt er die leere Menge in die Klasse $ss(a)$ ein. Damit erreicht er, dass $ss(a)$ mit Sicherheit nicht leer ist und dass $a$ ebenfalls problemslos aus $ss(a)$ zurückgewonnen werden kann.

Im letzten Schritt definiert Morse Klassenpaare $(a,b)$ als Vereinigung zweier kartesischer Produkte. Das erste kartesische Produkt enthält die Elemente von $ss(a)$ als Kuratowski-Paare, deren erstes Element stets gleich $\{\mathrm{\varnothing }\}$ ist. Das zweite kartesische Produkt enthält die Elemente von $ss(a)$ als Kuratowski-Paare, deren erstes Element stets gleich $\{\{\mathrm{\varnothing }\}\}$ ist. Das heißt, auch hier kann für jedes Element des $(a,b)$ eindeutig entschieden werden, ob es zur Klasse $a$ oder zur Klasse $b$ gehört. Die Eigenschaft, dass $ss(a)$ bzw. $ss(b)$ stets ungleich der leeren Menge ist, führt Morse ein, um sicherzustellen, dass das kartesische Produkt nicht leer ist (es gilt stets $x\times \mathrm{\varnothing }=\mathrm{\varnothing }$). Diese Vorsichtsmaßnahme wäre aber gar nicht nötig gewesen.

Man beachte, dass Morses Definition die Idee von Hausdorff zugrunde liegt: Er markiert die Elemente des ersten Paarelementes mit der leeren Menge, die als Zahl 0 interpretiert werden kann, und die Elemente des zweiten Paarmelementes mit der Menge $\{0\}$, die als Zahl 1 interpretiert werden kann.

Beispiel 3

	Notation	Definition	GlossarWiki-Definition
Schmidt (1966)	$(a,b)$	$(a,b):=\{\{\{x\}\}|x\in a\}\cup \{\mathfrak{P}(\{x\})|x\in b\}$	$\begin{array}{rcl}[a,b{]}_S& :=& \{\{\{x\}\}:x\in a\}\cup \{\mathcal{P}(\{x\}):x\in b\}\\ & =& \{\{\{x\}\}:x\in a\}\cup \{\{\mathrm{\varnothing },\{x\}\}:x\in b\}\end{array}$

Schmidt sagt von seiner Definition, sie sei an einen Vorschlag von Quine angelehnt. Er definiert Klassenpaare $(a,b)$ indem er, wie es von Quine in einer Fußnote in seinem Buch “Mathematical Logic” vorgeschlagen wurde, nicht die Klassen $a$ und $b$ selbst, sondern deren Elemente in einer Klasse zusammenfasst. Die Elemente der Klassen $a$ und $b$ unterscheidet Schmidt allerdings auf dieselbe Weise, wie Wiener Mengenpaar-Elemente unterscheidet.

Axiomatische Definition von geordneten Paaren

Geordnete Paare können axiomatisch als eigenständige Elemente in ein formales System eingefügt werden. Das wesentliche Axiom für geordnete Paare ist das Paaraxiom.

Beispiele

	Notation
Peano (1897)	$(a,b)$
von Neumann (1925)	$(a,b)$
McCarthy (1960, LISP)	$(a\cdot b)$ bzw. (a . b)
Oberschelp (1973) , Glubrecht, Oberschelp und Todt (1983): Klassenlogiken LE, LC, LA	<$a,b$>

Peano sowie Glubrecht, Oberschelp und Todt formulieren das Paaraxiom direkt, von Neumann und McCarthy fordern dagegen die Existenz von zwei Projektionsoperatoren, was – wie zuvor gezeigt wurde – ebenfalls die Erfüllung des Paaraxioms zur Folge hat.

Peano würde, wie bereits erwähnt wurde, auf eine axiomatische Defnition des Paarbegriffs gerne verzichten, weiß aber 1887 noch nicht, wie das gehen kann. John von Neumann verzichtet in späteren Arbeiten auf eine axiomatische Definition des Paarbegriffs. Er benutzt spätestens ab 1928 die Definition von Kuratowski.

John McCarthy sowie Glubrecht, Oberschelp und Todt sehen dagegen ganz bewusst geordnete Paare als primitive Elemente an, die nicht auf andere Elemente zurückgeführt werden. Für McCarthy sind die geordenten Paare („Cons-Zellen“) sowie die Urelemente („Atome“) die Basis sowohl der Sprache LISP als auch der zugehörigen Daten. Andere komplexe Datenstrukturen als geordnete Paare gibt es in McCarthys LISP nicht (sieh nachfolgenden Abschnitt).

Glubrecht, Oberschelp und Todt definieren so allgemeine klassenlogische Sprachen, dass sie auf eine Axiomatisierung des Paarberiffs nicht verzichten können. In der klassentheoretischen Logik LC unterscheiden sie beispielsweise nicht zwischen Mengen und Unmengen, sondern – allgemeiner – zwischen realen und virtuellen Objekten (S. 163). Klassen können sowohl reale, als auch virtuelle Objekte sein, Mengen sind dagegen reale Klassen, also reale Objekte (S. 187). Daneben gibt es auch Objekte, die weder Klassen oder gar Mengen sind. Individuen (= reale Objekte), die keine Elemente haben, heißen Urelemente (S. 187). Daneben kann es aber auch noch virtuelle Objekte geben, die keine Klassen sind. Ja, es kann sogar reale Objekte geben, die keine Urelemente und keine Klassen sind, und für die Elementbeziehungen bestehen:

Wir weisen noch einmal darauf hin, dass über Nichtklassen und die Elementbeziehung zu ihnen keinerlei Voraussetzungen gemacht werden. (S. 163)

In so einer allgemeinen logischen Sprache kann der Paarbegriff gar nicht auf Klassen oder gar Mengen zurückgeführt werden. Insbesondere virtuelle Nichtklassen könnten dann in keiner Paarbeziehung zu irgendwelchen Objekten stehen.

Noch allgemeiner ist Ausdruckslogik LA von Glubrecht, Oberschelp und Todt. In dieser Logik gibt es stets die beiden Urelemente $\mathrm{\top }$ und $\mathrm{\perp }$, die als „Wahr“ und „Falsch“ interpretiert werden. Junktoren ($\mathrm{\neg }$, $\wedge$, $\vee$ \etc.) gibt es dagegen nicht mehr. Diese werden mit Hilfe der Grundbegriffe „Gleichheit“ und „geordnetes Paar“ definiert: $\mathrm{\neg }a$ ist eine Abkürzung für $(a=\mathrm{\top })=\mathrm{\perp }$ und $a\wedge b$ ist eine Abkürzung für <$a,b$> = <$\mathrm{\top },\mathrm{\top }$>. Die übrigen Junktoren werden mit Hilfe von $\mathrm{\neg }$ und $\wedge$ definiert. Das heißt, die geordneten Paare werden benötigt, um die Sprache überhaupt definieren zu können. Daher können sie nicht ihrerseits auf andere Grundelemente zurückgeführt werden.

Geordnete Paare in der Informatik

Geordnete Paare und deren Verallgemeinerung, die Tupel, sind ein fundamentale Element, um in der Informatik komplexe Datenstrukturen definieren zu können.

Insbesondere in der Programmiersprache LISP sind die geordneten Paar das zentrale, ja sogar das einzige Elemnt, um komplexe Datenstrukturen zu definieren. Das Universum von LISP besteht aus “S-expressions”. Eine S-expression ist dabei entweder ein Atom (also ein Urelement) oder ein geordnetes Paar (a . b), dessen beiden Elemente a und b S-expressions sind. Tupel (= geordnete Listen), Funktionen und Mengen werden später auf Basis dieses Universums eingeführt: Eine LISP-Liste (a b c) $:=$ (a . ( b . (c . NIL))) ist eine Folge von geordneten Paaren, wobei NIL ein atomares Element ist. Funktionen sind Lamda-Terme, die mit Hilfe von Listen dargestellt werden (z. B. (lambda (x) (+ x 1))). Die Semantik dieser Funktionen wird mit Hilfe des Lamda-Kalküls festgelegt. Und Mengen sind Listen, für die spezielle Mengenfunktionen definiert sind (siehe z. B. Common Lisp).

Aber auch in allen anderen Programmiersprachen gibt es Tupel, das heißt geordnete Paare, Tripel, Quadrupel etc. Mit Ausnahme von SQL werden die Tupel jedoch meist anders bezeichnet: Record, Array, Object, Map ...

Die wichtigsten funktionalen Definitionen des geordneten Paars

TO BE DONE

Diesen Abschnitt in einzelen Seiten auslagern.

Heute werden Paare meist als Mengen- oder Klassenpaare definiert. Aber auch in Mengenlehresystemen, in denen „Funktion“ der unbestimmte Grundbegriff ist, dessen Eigenschaften axiomatisch festgelegt werden und mit dessen Hilfe die übrigen Begriffe, wie „Menge“, „Klasse“, „Relation“ etc. definiert werden, ist es möglich, „geordnete Paare“ einzuführen. Insbesondere Gottlob Frege und Alonzo Church sind diesen Weg gegangen.

Frege benötigt Paare zur Konstruktion von reellen Zahlen (vgl. Frege (1903, §161 ff.), Kutschera (1989, S. 125)). Er war mit seinem strengen Formalismus seiner Zeit weit voraus ) und führte daher den Paarbegriff, wie auch alle anderen von ihm verwendeten Begriffe, streng formal ein.

Definition des geordneten Paars, Frege (1893), §144, S. 179

Frege (1893)

Wir definiren nun das Paar so:

$⊩\acute{ϵ}(o⌢(a⌢ϵ))=o;a$

Das Semikolon ist hierbei zweiseitiges Functionszeichen. (§144, S. 179)

Frege definiert keine Projektionsoperatoren. Folgende Definition stammt von W. Kowarschick (siehe Geordnetes Paar: Definition von Frege):

$\begin{array}{l}⊩\acute{p}(p(\acute{x}(\acute{y}y)))={\pi }_1\\ ⊩\acute{p}(p(\acute{x}(\acute{y}x)))={\pi }_2\end{array}$

Anmerkungen

$⊩$ ist bei Frege der „Definitionsdoppelstrich“ und $\acute{ϵ}\varphi (ϵ)$ der „Werthverlauf“ einer Funktion $\varphi$, wobei man den Wertverlauf-Operator als Lambda-Operator vorstellen kann:

$\acute{ϵ}\varphi (ϵ)\hat{\approx }\lambda ϵ.\varphi (ϵ)$

$⌢$ ein ein Operator, der den Funktionsaufruf für Wertverläufe nachbildet:

Satz 1 und Satz 2: Der Wertverlauf von ein- und zweistelligen Funktionen, Frege (1893), S. 75

$⊢f(a)=a⌢\acute{ϵ}f(ϵ)$ (Frege: Satz 1, §54, S. 75)

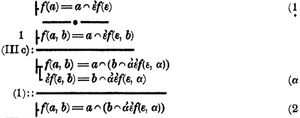
Das Symbol $⊢$ ist dabei der „Inferenzoperator“, der schon bei Frege die heute noch übliche Bedeutung hatte: Aus den Axiomen kann die nachfolgende Formel logisch hergeleitet werden.

Wenn man die η-Konversion im Lambda-Kalkül zulässt, kann man den Wertverlauf von $\varphi$ mit $\varphi$ identifizieren (Frege unterscheidet allerdings streng zwischen Funktion und zugehörigem Wertverlauf):

$\lambda ϵ.\varphi (ϵ)=\varphi$

In diesem Fall gilt:

$(\lambda ϵ.\varphi (ϵ))(x)=\varphi (x)$

Das heißt, der $⌢$-Oerator entspricht im Prinzip der $\beta$-Konversion. Freges Paar-Definition kann also folgendermaßen im Lambda-Kalkül nachgebildet werden:

$o;a:=\lambda ϵ.ϵao$

Eine detailierte Diskussion von Freges Definition findet sich im Artikel Geordnetes Paar: Definition von Frege.

Freges Definition ist die älteste mir bekannte Definition, die den Paarbegriff auf zuvor definierte Grundbegriffe zurückführt. Allerdings ist diese Definition nicht dazu geeignet, Relationen und Funktionen zu definieren, weil sie den Funktionsbegriff als gegeben voraussetzt. Dies war aber auch nicht die Absicht von Frege. Er benötigte die Paare zur Konstruktion von reellen Zahlen (vgl. Frege (1903, §161 ff.), Kutschera (1989, S. 125)).

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Projektionsoperatoren. Der Beweis des Satzes basiert im Wesentlichen auf Satz 1 von Frege.

$\begin{array}{lcll}{\pi }_1(a;b)& =& \acute{p}(p(\acute{x}(\acute{y}y)))(a;b)& (\mathrm{D}\mathrm{e}\mathrm{f}.\mathrm{v}\mathrm{o}\mathrm{n}{\pi }_1)\\ & =& (a;b)⌢\acute{p}(p(\acute{x}(\acute{y}y)))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& (a;b)(\acute{x}(\acute{y}y))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& \acute{x}(\acute{y}y)⌢(a;b)& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& \acute{x}(\acute{y}y)⌢(\acute{ϵ}(a⌢(b⌢ϵ))& (\mathrm{D}\mathrm{e}\mathrm{f}.\mathrm{v}\mathrm{o}\mathrm{n}\mathrm{a};\mathrm{b})\\ & =& a⌢(b⌢\acute{x}(\acute{y}y))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& a⌢\acute{y}y& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& a& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ {\pi }_2(a;b)& =& \acute{p}(p(\acute{x}(\acute{y}x)))(a;b)& (\mathrm{D}\mathrm{e}\mathrm{f}.\mathrm{v}\mathrm{o}\mathrm{n}{\pi }_2)\\ & =& (a;b)⌢\acute{p}(p(\acute{x}(\acute{y}x)))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& (a;b)(\acute{x}(\acute{y}x))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& \acute{x}(\acute{y}x)⌢(a;b)& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& \acute{x}(\acute{y}x)⌢(\acute{ϵ}(a⌢(b⌢ϵ))& (\mathrm{D}\mathrm{e}\mathrm{f}.\mathrm{v}\mathrm{o}\mathrm{n}\mathrm{a};\mathrm{b})\\ & =& a⌢(b⌢\acute{x}(\acute{y}x))& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& a⌢\acute{y}b& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\\ & =& b& (\mathrm{F}\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{e}:\mathrm{S}\mathrm{a}\mathrm{t}\mathrm{z}1)\end{array}$

Das Paaraxiom

Freges Paar-Begriff erfüllt das Paaraxiom, Frege (1893), Tafel der wichtigeren Lehrsätze, S. 248

Frege beweist mit Hilfe der von ihm definerten Axiome mehrere Paareigenschaften. Die wichtigsten dieser Sätze sind (in moderner Notation):

$⊢a=i\to (o=e\to o;a=e;i)$ (Frege (1893), §155, Satz Nr. 251; Tafel der wichtigeren Lehrsätze, S. 248)

Wenn ein Gegenstand mit einem zweiten und ein dritter Gegenstand mit einem vierten zusammenfällt, so fällt das aus dem ersten und dritten bestehende Paar zusammen mit dem aus dem zweiten und vierten bestehenden.

$⊢m;x=c;d\to x=d$ (Frege (1893), §149, Satz Nr. 219; Tafel der wichtigeren Lehrsätze, S. 248)

Wenn ein Paar mit einem zweiten zusammenfällt, so fällt das zweite Glied des ersten mit dem zweiten Gliede des zweiten zusammen.

$⊢m;x=c;d\to m=c$ (Frege (1893), §149, Satz Nr. 220; Tafel der wichtigeren Lehrsätze, S. 248)

(ohne weitere Erörterungen von Frege)

Diese Eigenschaften zeigen, dass sein Paarbegriff das Paaraxiom erfüllt, welches explizit erst vier Jahre später von Giuseppe Peano formuliert wurde.

Church (1941)

TO BE DONE

Die wichtigsten Definitionen von Mengenpaaren

Im Folgenden werden wegweisende Definitionen von Mengenpaaren (d. h. Unmengen sind als Paarelemente nicht erlaubt) aufgeführt: die Definitionen von Hausdorff, Wiener, Kuratowski und Quine. Es werden jeweils auch die beiden Projektionsoperatoren angegeben. Gemäß Satz 6.2 („Aus der Existenz der Projektionsoperatoren folgt das Paaraxiom“) ist damit sichergestellt, dass das Paaraxiom erfüllt ist.

Definition des geordneten Paars mit Hilfe von Mengen, Hausdorff (1914), S. 32

Hausdorff (1914)

Felix Hausdorff unterscheidet das erste und das zweite Element eines Paares mit Hilfe zweier spezieller Mengen $\mathbf{1}$ und $\mathbf{2}$, die anderweitig nicht verwendet werden. Es sei $\{a,b\}\cap \{\mathbf{1},\mathbf{2}\}=\mathrm{\varnothing }\wedge \mathbf{1}\ne \mathbf{2}$ erfüllt.

$\begin{array}{lcl}[a,b]& :=& \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\\ {\pi }_1(p)& :=& \bigcap \{x|\{x,\mathbf{1}\}\in p\}\\ {\pi }_2(p)& :=& \bigcap \{x|\{x,\mathbf{2}\}\in p\}\end{array}$

Anmerkungen zur Definition von Hausdorff

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Mengenpaar-Operatoren:

$\begin{array}{lcl}{\pi }_1([a,b])& =& \bigcap \{x|\{x,\mathbf{1}\}\in [a,b]\}\\ & =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\}\\ & =& \bigcap \{a\}& \text{(da }b\ne \mathbf{1}\text{ und da }a,b\text{ Mengen sind)}\\ & =& a& \text{(da }a\text{ eine Menge ist)}\\ {\pi }_2([a,b])& =& \bigcap \{x|\{x,\mathbf{2}\}\in [a,b]\}\\ & =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\}\\ & =& \bigcap \{b\}& \text{(da }a\ne \mathbf{2}\text{ und da }a,b\text{ Mengen sind)}\\ & =& b& \text{(da }b\text{ eine Menge ist)}\end{array}$

Diese Definition hat einen Nachteil. Um den Paarbegriff verwenden zu können, muss man für die Elemente, die in Paaren gespeichert werden sollen, gemäß der Definition von Hausdorff stets voraussetzen, dass diese Elemente ungleich $\mathbf{1}$ und ungleich $\mathbf{2}$ sind. Derartige Fallunterscheidungen blähen die zugehörigen Beweise unnötig auf.

Allerdings ist die von Hausdorff geforderte Bedingung $\{a,b\}\cap \{\mathbf{1},\mathbf{2}\}=\mathrm{\varnothing }$ unnötig. Es reicht aus, wenn $\mathbf{1}\ne \mathbf{2}$ erfüllt ist.

Es gelte für die folgenden Betrachtungen zunächst noch $\{a,b\}\cap \{\mathbf{1},\mathbf{2}\}=\mathrm{\varnothing }$. Dann kann man folgende Fälle unterscheiden:

$\begin{array}{rlclcl}1.& [a,\mathbf{1}]& =& \{\{a,\mathbf{1}\},\{\mathbf{1},\mathbf{2}\}\}& =& \{\{\mathbf{1},\mathbf{2}\},\{a,\mathbf{1}\}\}\\ 2.& [a,\mathbf{2}]& =& \{\{a,\mathbf{1}\},\{\mathbf{2},\mathbf{2}\}\}& =& \{\{a,\mathbf{1}\},\{\mathbf{2}\}\}\\ 3.& [a,b]& =& \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}& =& \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\\ 4.& [\mathbf{1},b]& =& \{\{\mathbf{1},\mathbf{1}\},\{b,\mathbf{2}\}\}& =& \{\{\mathbf{1}\},\{b,\mathbf{2}\}\}\\ 5.& [\mathbf{2},b]& =& \{\{\mathbf{2},\mathbf{1}\},\{b,\mathbf{2}\}\}& =& \{\{\mathbf{1},\mathbf{2}\},\{b,\mathbf{2}\}\}\\ 6.& [\mathbf{1},\mathbf{2}]& =& \{\{\mathbf{1},\mathbf{1}\},\{\mathbf{2},\mathbf{2}\}\}& =& \{\{\mathbf{1}\},\{\mathbf{2}\}\}\\ 7.& [\mathbf{2},\mathbf{1}]& =& \{\{\mathbf{2},\mathbf{1}\},\{\mathbf{1},\mathbf{2}\}\}& =& \{\{\mathbf{1},\mathbf{2}\}\}\end{array}$

Wie man sieht, unterscheiden sich alle Mengen auf der rechten Seite. Es gibt nur drei Mengen, die zwei zweielementige Mengen enthalten (1., 3, und 5.). Diese drei Mengen unterscheiden sich jedoch. Es gibt darüber hinaus zwei wohlunterscheidbare Mengen, die je eine zwei- und eine einelementige Menge enthalten (2. und 4.). Die beiden letzen Mengen sind ebenfalls einmalig: 6. ist eine zweielementige Menge, deren beiden Elemente einelementig sind, und 7. ist eine einelementige Menge, die eine zweielementige Menge enthält.

Verallgemeinerung der Projektionsoperatoren

Wenn man die Projektionsoperatoren auf alle sieben unterschiedlichen Fälle anwendet, stellt man fest, dass jeweils nur in einem Fall ein falsches Ergebnis geliefert wird.

$\begin{array}{rlclclclclcl}1.& {\pi }_1([a,\mathbf{1}])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{\mathbf{1},\mathbf{2}\},\{a,\mathbf{1}\}\}\}& =& \mathrm{\varnothing }& & {\pi }_2([a,\mathbf{1}])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{\mathbf{1},\mathbf{2}\},\{a,\mathbf{1}\}\}\}& =& \mathbf{1}\\ 2.& {\pi }_1([a,\mathbf{2}])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{a,\mathbf{1}\},\{\mathbf{2}\}\}\}& =& a& & {\pi }_2([a,\mathbf{2}])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{a,\mathbf{1}\},\{\mathbf{2}\}\}\}& =& \mathbf{2}\\ 3.& {\pi }_1([a,b])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\}& =& a& & {\pi }_2([a,b])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{a,\mathbf{1}\},\{b,\mathbf{2}\}\}\}& =& b\\ 4.& {\pi }_1([\mathbf{1},b])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{\mathbf{1}\},\{b,\mathbf{2}\}\}\}& =& \mathbf{1}& & {\pi }_2([\mathbf{1},b])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{\mathbf{1}\},\{b,\mathbf{2}\}\}\}& =& b\\ 5.& {\pi }_1([\mathbf{2},b])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{\mathbf{1},\mathbf{2}\},\{b,\mathbf{2}\}\}\}& =& \mathbf{2}& & {\pi }_2([\mathbf{2},b])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{\mathbf{1},\mathbf{2}\},\{b,\mathbf{2}\}\}\}& =& \mathrm{\varnothing }\\ 6.& {\pi }_1([\mathbf{1},\mathbf{2}])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{\mathbf{1}\},\{\mathbf{2}\}\}\}& =& \mathbf{1}& & {\pi }_2([\mathbf{1},\mathbf{2}])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{\mathbf{1}\},\{\mathbf{2}\}\}\}& =& \mathbf{2}\\ 7.& {\pi }_1([\mathbf{2},\mathbf{1}])& =& \bigcap \{x|\{x,\mathbf{1}\}\in \{\{\mathbf{1},\mathbf{2}\}\}\}& =& \mathbf{2}& & {\pi }_2([\mathbf{2},\mathbf{1}])& =& \bigcap \{x|\{x,\mathbf{2}\}\in \{\{\mathbf{1},\mathbf{2}\}\}\}& =& \mathbf{1}\end{array}$

Der Projektionsoperator ${\pi }_1$ liefert nur im ersten Fall ein fehlerhaftes Ergebnis. Analog ist das Ergebnis von ${\pi }_2$ im fünften Fall falsch. Dies kann aber problemlos behoben werden:

$\begin{array}{lcl}{\pi }_1(p)& :=& \bigcap (\{x|\{x,\mathbf{1}\}\in p\}\cup \{x|x\notin \{\mathbf{1},\mathbf{2}\}\wedge \bigvee y:\{x,y\}\in p\wedge y=\mathbf{1}\})\\ {\pi }_2(p)& :=& \bigcap (\{x|\{x,\mathbf{2}\}\in p\}\cup \{x|x\notin \{\mathbf{1},\mathbf{2}\}\wedge \bigvee y:\{x,y\}\in p\wedge y=\mathbf{2}\})\end{array}$

Wiener (1914)

Bei der Definition von Norbert Wiener besteht der (vermeindliche) Nachteil der Hausdorff-Paare nicht, da er das erste und und das zweites Element eines Paares anhand der Mächtigkeit der zugehörigen Mengen unterscheidet: $a$ ist Element einer einelementigen Menge und $b$ ist Element einer zweielementigen Menge.

$\begin{array}{lcl}[a,b]& :=& \{\{\{a\}\},\{\mathrm{\varnothing },\{b\}\}\}\\ {\pi }_1(p)& :=& \bigcap \{x\{\{x\}\}\in p\}\\ {\pi }_2(p)& :=& \bigcap \{x|\{\mathrm{\varnothing },\{x\}\}\in p\}\end{array}$

Anmerkungen zur Definition von Wiener

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Mengenpaar-Operatoren:

$\begin{array}{lcl}{\pi }_1([a,b])& =& \bigcap \{x|\{\{x\}\}\in [a,b]\}\\ & =& \bigcap \{x|\{\{x\}\}\in \{\{\{a\}\},\{\mathrm{\varnothing },\{b\}\}\}\}\\ & =& \bigcap \{a\}& \text{(da }a,b\text{ Mengen sind)}\\ & =& a& \text{(da }a\text{ eine Menge ist)}\\ {\pi }_2([a,b])& =& \bigcap \{x|\{\mathrm{\varnothing },\{x\}\}\in [a,b]\}\\ & =& \bigcap \{x|\{\mathrm{\varnothing },\{x\}\}\in \{\{\{a\}\},\{\mathrm{\varnothing },\{b\}\}\}\}\\ & =& \bigcap \{b\}& \text{(da }a,b\text{ Mengen sind)}\\ & =& b& \text{(da }b\text{ eine Menge ist)}\end{array}$

Die Definition von Wiener sorgt dafür, dass die Menge $\{\mathrm{\varnothing },\{b\}\}$ auch im Fall $b=\mathrm{\varnothing }$ zweielementig ist. Für $\{\mathrm{\varnothing },b\}$ wäre dies dagegen nicht der Fall.

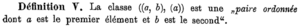
Geordnetes Paar mit Hilfe von Menge, Kuratowski (1921), S. 171

Kuratowski (1921)

Kazimierez Kuratowski definiert sieben Jahre später geordnete Mengenpaare deutlich einfacher als Wiener und Hausdorff. (Er geht in seinen Artikel allerdings nur auf die Vorteile seiner Definition gegenüber der Definition von Hausdorff ein.)

La classe $((a,b),(a))$ est une „paire ordonnée dont $a$ est le premier élément et $b$ est le second“.

Übersetzung:

Die Klasse $((a,b),(a))$ ist ein „geordnetes Paar, wobei $a$ das erste Element ist und $b$ das zweite“.

Moderne Schreibweise:

$\begin{array}{lcl}[a,b]& :=& \{\{a\},\{a,b\}\}\\ {\pi }_1(p)& :=& \bigcap \bigcap p& =& \bigcup \bigcap p\\ {\pi }_2(p)& :=& \bigcap (\{x\in \bigcup p|\bigcup p\ne \bigcap p\to x\notin \bigcap p\})& =& \bigcup (\{x\in \bigcup p|\bigcup p\ne \bigcap p\to x\notin \bigcap p\})\end{array}$

Anmerkungen zur Definition von Kuratowski

Allgemein gilt für Mengen $a$:

$\begin{array}{lclcl}\bigcap \{a\}& =& \bigcup \{a\}& =& a\end{array}$

Kuratowski-Paare haben folgende Eigenschaften, da $a$ und $b$ Mengen sind:

$\begin{array}{lclcl}\bigcap [a,b]& =& \bigcap \{\{a\},\{a,b\}\}& =& \{a\}\\ \bigcup [a,b]& =& \bigcup \{\{a\},\{a,b\}\}& =& \{a,b\}\end{array}$

Damit kann man zeigen, dass es sich bei ${\pi }_1$ und ${\pi }_2$ tatsächlich um Paaroperatoren handelt:

$\begin{array}{lcl}{\pi }_1([a,b])& =& \bigcap \bigcap [a,b]\\ & =& \bigcap \{a\}& \text{(anstelle von }\bigcap \text{ könnte man auch }\bigcup \text{ verwenden)}\\ & =& a& \text{(da }a\text{ eine Menge ist)}\\ {\pi }_2([a,b])& =& \bigcap (\{x\in \bigcup [a,b]:\bigcup [a,b]\ne \bigcap [a,b]\to x\notin \bigcap [a,b]\})\\ & =& \bigcap (\{x\in \{a,b\}:\{a,b\}\ne \{a\}\to x\notin \{a\}\})\\ & =& \bigcap \{b\}& \text{(anstelle von }\bigcap \text{ könnte man auch }\bigcup \text{ verwenden)}\\ & =& b& \text{(da }b\text{ eine Menge ist)}\end{array}$

Alternativ könnte ${\pi }_2$ folgendermaßen definiert werden:

$\begin{array}{lcl}{\pi }_2(p)& :=& \{\begin{array}{ll}\bigcap \bigcup p& \text{falls }\bigcup p=\bigcap p\\ \bigcap (\bigcup p\setminus \bigcap p)& \text{falls }\bigcup p\ne \bigcap p\end{array}\end{array}$

Die Bedingung $\bigcup p\ne \bigcap p$ bei der Definition von ${\pi }_2$ wird benötigt, damit ${\pi }_2$ auch für Paare der Art $[a,a]$ das korrekte zweite Element $a$ berechnet. Würde man diese Bedingung weglassen, würde ${\pi }_2([a,a])=\mathrm{\varnothing }$ gelten.

Nelson Goodman merkt an, dass sich die Definition von Kuratowski problemlos für beliebige $n$-Tutpel (wobei $n$ eine natürliche, d. h. endliche Zahl ist) verallgemeinern lässt. Er gibt allerdings kein allgemeines Konstruktionsprinzip, sondern nur folgendes Beispiel an:

$\begin{array}{lcl}[a,b,c]& :=& \{\{\{a\}\},\{\{a,b\}\},\{\{a,b\},\{c\}\}\}\end{array}$

Anmerkungen zum geordneten Paar, Quine (1981), S. 201 und S. 202, erstmals 1940 pubiziert

Quine (1940)

Willard Quine merkt in seinem Buch „Mathematical Logic“ an, dass Wieners Definition vereinfacht werden kann. (Er verwendet dennoch die Definition von Kuratowski und schlägt außerdem eine erste Klassenpaar-Definition vor, die er allerdings selbst kurz darauf als fehlerhaft erkennt; vgl. Abschnitt „Die Weiterentwicklung des Paarbegriffs“.)

$\begin{array}{lcl}[a,b]& :=& \{\{a\},\{\mathrm{\varnothing },b\}\}\\ {\pi }_1(p)& :=& \bigcap \{x|\{x\}\in p\}\\ {\pi }_2(p)& :=& \bigcap \{x|\{\mathrm{\varnothing },x\}\in p\}\end{array}$

Quine (1986)

Quine definiert Mengenpaare wie folgt, wobei $0:=\mathrm{\varnothing }$, $1:=0\cup \{0\}=\{\mathrm{\varnothing }\}$ und $2:=1\cup \{1\}=\{\mathrm{\varnothing },\{\mathrm{\varnothing }\}\}$:

$\begin{array}{rcl}[a,b]& :=& \{\{\{a\},1\},\{\{b\},2\}\}\\ {\pi }_1(p)& :=& \bigcap \{x|\{\{x\},1\}\in p\}\\ {\pi }_2(p)& :=& \bigcap \{x|\{\{x\},2\}\in p\}\end{array}$

Anmerkungen zur Definition von Quine

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Paaroperatoren, da $a$ und $b$ Mengen sind:

$\begin{array}{rclrrrr}{\pi }_1([a,b])& =& \bigcap \{x|\{\{x\},1\}\in [a,b]\}& =& \bigcap \{a\}& =& a\\ {\pi }_2([a,b])& =& \bigcap \{x|\{\{x\},2\}\in [a,b]\}& =& \bigcap \{b\}& =& b\end{array}$

In den 40er-Jahren hatte Willard Quine eine Klassenpaar-Definition entwickelt (siehe Abschnitt Weiterentwicklung des Paarbegriffs), die sich problemlos zu einer Definition von $n$-Tupeln ($n\in \mathbb{N}$) verallgemeinern lässt, wobei $n\in \omega$ eine natürliche Zahl ist. 1986 schlägt er die obige Mengenpaar-Definition vor, bei der es sich um eine leicht modifizierte Version der Hausdorff-Paare handelt. Diese ist zwar nicht für Unmengen definiert, lässt sich dafür aber nicht nur zu einer Definition von $n$-Tupeln verallgemeinern,

$[a_1,\dots ,a_n]:=\{\{\{a_1\},1\},\dots ,\{\{a_n\},n\}\}$

sondern sogar zu einer Definition von $o$-Tupeln, wobei $o\in \mathrm{\Omega }$ eine beliebige Ordinalzahl ist. Diese werden gemäß dem Vorschlag von John von Neumann folgendermaßen definiert:

$0:=\{\}$

$1:=0\cup \{0\}=\{\{\}\}$

$2:=1\cup \{1\}=\{0,1\}=\{\{\},\{\{\}\}\}$

$3:=2\cup \{2\}=\{0,1,2\}=\{\{\},\{\{\}\},\{\{\},\{\{\}\}\}\}$

$⋮$

$\omega :=\{0,1,2,\dots \}$

$\omega +1:=\omega \cup \{\omega \}$

$\omega +2:=\omega +1\cup \{\omega +1\}$

$⋮$

Die Idee hinter Quines Definition ist, dass jedem Paar- bzw. Tupelelement seine Position im $o$-Tupel mit Hilfe einer Ordinalzahl $p$ zugeordnet wird. Dabei werden nicht die Mengenpaare $\{x,p\}$ gebildet, sondern die Mengenpaare $\{\{x\},p\}$, da es anderenfalls zu Mehrdeutigkeiten im Falle von $x\in \mathrm{\Omega }$ kommen würde. Beim Mengenpaar $\{2,3\}$ wäre beispielsweise nicht klar, ob es sich um die Zahl $2$ an der Postion $3$ handelt oder um die Zahl $3$ an der Position $2$. Beim $\{\{2\},3\}$ ist dagegen eindeutig bestimmt, dass es sich um die Zahl $2$ an der Postion $3$ handelt.

Quine betont, dass $1=\{0\}$ die einzige einelementige (John-von-Neumann-)Ordinalzahl ist. Also könnte es nur im Zusammenhang mit der Ordinalzahl $0$ zu Mehrdeutigkeiten kommen:

$\begin{array}{rclcl}[a,0]& =& \{\{\{a\},1\},\{\{0\},2\}\}& =& \{\{\{a\},1\},\{1,2\}\}\\ [0,b]& =& \{\{\{0\},1\},\{\{b\},2\}\}& =& \{\{1,1\},\{\{b\},2\}\}& =& \{\{1\},\{\{b\},2\}\}\end{array}$

Allerdings liefern die Projektionsoperatoren auch in diesen Fällen das korrekte Ergebnis, da $2=\{0,1\}$ zweielementig ist:

$\begin{array}{rclclcl}{\pi }_1([a,0])& =& \bigcap \{x|\{\{x\},1\}\in \{\{\{a\},1\},\{\{0\},2\}\}& =& \bigcap \{a\}& =& a\\ {\pi }_1([0,b])& =& \bigcap \{x|\{\{x\},1\}\in \{\{\{0\},1\},\{\{b\},2\}\}& =& \bigcap \{0\}& =& 0\\ {\pi }_2([a,0])& =& \bigcap \{x|\{\{x\},2\}\in \{\{\{a\},1\},\{\{0\},2\}\}& =& \bigcap \{0\}& =& 0\\ {\pi }_2([0,b])& =& \bigcap \{x|\{\{x\},2\}\in \{\{\{0\},1\},\{\{b\},2\}\}& =& \bigcap \{b\}& =& b\end{array}$

Die wichtigsten Definitionen von Klassenpaaren

Wenn Paare nicht nur Mengen, sondern auch Unmengen enthalten können, spricht man von Klassenpaaren.

Die Definitionen von Wiener, Hausdorff und Kuratowski sind für Klassenpaare allerdings ungeeignet, da diese Definitionen alle darauf basieren, dass die Paarelemente $a$ und $b$ Elemente von ein- und/oder zweielementigen Mengen sind. Unmengen können jedoch – gemäß ihrer Definition – nicht Elemente von irgendwelchen Mengen sein:

$\bigwedge u:\mathrm{U}\mathrm{M}\mathrm{g}(\mathrm{u})\to \{\mathrm{u}\}=\mathcal{V}$ (siehe Definition von $n$-elementigen Mengen)

Und da die Allklasse selbst wieder ein Unmenge ist, pflanzt sich die Unmengeneingeschaft fort, wenn nur ein einziges Element einer beliebigen Klasse eine Unmenge ist.

Auch wenn $\{u\}$ für Unmengen anders definiert werden sollte (wie z. B. $\{u\}=\mathrm{\varnothing }$; siehe Alternative Definition einer einelementigen Menge), wäre nichts gewonnen. Da sich Klassen, die Unmengen als Elemente enthalten, für verschiedene Unmengen nicht voneinander unterscheiden, unterscheiden sich auch die entsprechenden Mengenpaar-Definitionen auch nicht.

Man kann sich das Problem der Unmengen auch anhand der Typtheorie verdeutlichen. Wie im Abschnitt „Die Weiterentwicklung des Paarbegriffs“ beschrieben wurde, liegen die Mengenpaare von Hausdorff, Wiener und Kuratowski auf einer höheren Ebene als ihre Elemente. Eine Unmenge liegt dagegen auf gar keiner Ebene. Für jede Ebene gibt es beliebig viele Elemente der Unmenge, die auf höheren Ebenen liegen. Also kann eine Paardefinition, bei dem jedem Paar eine Ebene zugeordnet werden kann, hier nicht funktionieren.

In einem mengenbasiertes Axiomen-System (wie es z. B. der Zermelo-Fraenkel-Mengenlehre zu Grunde liegt) ist das Paaraxiom

$\bigwedge a,b:[a,b]=[b,a]\leftrightarrow a=b$

für Mengenpaare uneingeschränkt gültig, da in diesem Fall $\bigwedge$ als „Für alle Mengen innerhalb des Mengenuniversums“ interpretiert wird. In einem klassenbasierten Axiomen-System (wie es z. B. der Neumann-Bernays-Gödel-Mengenlehre zu Grunde liegt) wird $\bigwedge$ jedoch als „Für alle Klassen, d. h. für alle Mengen und Unmengen innerhalb des Klassenuniversums“ interpretiert. Für die bislang definierten Mengenpaare gilt in derartigen Systemen lediglich:

$\bigwedge a,b:\mathrm{M}\mathrm{g}(\mathrm{a})\wedge \mathrm{M}\mathrm{g}(\mathrm{b})\to ([\mathrm{a},\mathrm{b}]=[\mathrm{b},\mathrm{a}]\leftrightarrow \mathrm{a}=\mathrm{b})$

Für die Definition von Relationen und Funktionen reicht diese eingeschränkte Form des Paaraxioms aus. Relationen und Funktionen anhalten Paare (oder – allgemeiner – Tupel) als Elemente. Auch wenn eine Relation oder eine Funktion selbst eine Unmenge sein sollte, so sind doch alle ihre Elemente Mengen.

Wenn man allerdings beispielsweise Algebren, wie die Halbgruppe der Ordinalzahlen $\mathrm{\Omega }$ mit Addition $+$ als $2$-Tupel, d. h. als geordnetes Paar $[\mathrm{\Omega },+]$ definieren will, reicht das eingeschränkte Paaraxiom nicht mehr aus. Die Klasse der Ordinalzahlen $\mathrm{\Omega }$ ist eine Unmenge.

Quine (1945)

Zunächst wird zur Abkürzung der nachfolgenden Definitionen eine Hilfsoperationen eingeführt (die allerdings jederzeit durch Textersetzung eliminiert werden kann):

$\begin{array}{lclcl}\theta (z)& :=& \{v|v\in z\wedge v\notin \mathbb{N}\}\cup \{v+1|v\in z\wedge v\in \mathbb{N}\}& =& (z\setminus \mathbb{N})\cup \{n+1|n\in (z\cap \mathbb{N})\}\end{array}$

Mit Hilfe der Operation $\theta$ definiert Willard Quine geordnete Paare wie folgt:

$\begin{array}{rcl}[a,b]& :=& \{\theta (x):x\in a\}\cup \{\theta (x)\cup \{0\}:x\in b\}\\ {\pi }_1(p)& :=& \{x|\theta (x)\in p\}\\ {\pi }_2(p)& :=& \{x|\theta (x)\cup \{0\}\in p\}\end{array}$

Anmerkungen zu Quines Definition von 1945

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Paaroperatoren:

$\begin{array}{rclcl}{\pi }_1([a,b])& =& \{x|\theta (x)\in [a,b]\}& =& a\\ {\pi }_2([a,b])& =& \{x|\theta (x)\cup \{0\}\in [a,b]\}& =& b\end{array}$

Rosser-Paare

1953 übernimmt J. Barkley Rosser die Definition von Quine. Die oben angegebenen Projektionsoperatoren stammen von ihm. Quine hat nur deren Existenz postuliert (siehe nachfolgenden Abschnitt).

Die Idee hinter Quines Definition

Um Paare $[a,b]$ auf dieselbe Ebene zu legen wie ihre Elemente $a$ und $b$, fügt Willard Quine nicht $a$ und $b$ selbst, sondern deren Elemente in die zugehörige Paarmenge ein. Dazu definiert er zunächst die Operation $\theta (z)$ (er spricht nicht von „operator“ sondern von „notion“), die die Elemente der Menge $z$ leicht modifiziert, indem sie alle natürlichen Zahlen, die in $z$ enthalten sind, um eins erhöht. Man beachte, dass es sich bei $\theta (z)$ um keine Funktion handelt, da Funktionen erst in einem zweiten Schritt mit Hilfe von geordneten Paaren definiert werden. Es handelt sich vielmehr um eine abkürzende Schreibweise, die jederzeit durch Ersetzung eliminiert werden kann.

$\theta (z)$ hat laut Quine folgende Eigenschaften:

1. Es gibt kein $z$ für das $0\in \theta (z)$ gilt; $0$ ist dabei die natürliche Zahl „Null“.
2. Aus $\theta (z)$ lässt sich $z$ eindeutig ermitteln.
3. $z$ und $\theta (z)$ liegen auf derselben Ebene in der Typhierachie.

Da der Nachfolger einer jeden natürlichen Zahl ungleich $0$ ist, enthält $\theta (z)$ mit Sicherheit nicht die Zahl $0$, erfüllt also die erste Bedingung. Die zweite Bedingung ist ebenfalls erfüllt, da sich $z$ problemlos aus $\theta (z)$ ableiten lässt. Man braucht nur jede natürliche Zahl in $\theta (z)$ um eins zu veringern.

Die dritte Bedingung zu erfüllen, ist etwas komplizierter. Die Bedingung ist beispielsweise erfüllt, wenn man der Mengenlehre eine Typhierarchie mit natürlichen Zahlen als Urelementen zu Grunde legt.

Quine führt allerdings die natürliche Zahl $0$, die Nachfolgeroperation $n+1$ und die Menge aller natürlichen Zahlen $\mathbb{N}$ (er wählt in beiden Fällen andere Symbole) induktiv ein. Er macht dies so geschickt, dass eine natürliche Zahl $n$ und ihr Nachfolger $n+1$ – bezüglich der vom ihm definierten Typhierarchie – stets vom selben Typ sind, d. h. stets auf derselben Ebene liegen.

Quine-Paare (gemäß der Definition von 1945) sind Klassenpaare

Quines Idee, nicht die Paarelemente $a$ und $b$ selbst, sondern deren Elemente in der Paarklasse zu „speichern“, hat insbesondere zur Folge, dass auch Unmengen als Paarelemente fungieren können. Unmengen enhalten zwar ausschließlich Elemente, können selbst aber keine Elemente sein. Das heißt, Unmengen können nur rechts vom Elementzeichen $\in$ vorkommen. Und das ist bei Quines Definition gegeben: $a$ und $b$ stehen nur rechts vom Element-Operator.

Das Paaraxiom ist also im Falle von Quine-Paare nicht nur für Mengen, sondern auch für Unmengen erfüllt. Das heißt, Quine-Paare sind – sowohl in der Version von 1945 als auch schon in der Version von 1941 – Klassenpaare.

Dabei ist es vollkommen unwichtig, auf welche Art die natürlichen Zahlen, die im Operator $\theta$ verwendet werden, repräsentiert werden. Heute verwendet man überlicherweise die Repräsentation, die John von Neumann vorgeschlagen hat (siehe Abschnitt „Anmerkungen zur Definition von Quine“). Und es ist auch unwichtig, ob die Bedingung „$z$ und $\theta (z)$ liegen auf derselben Ebene in der Typhierachie“ erfüllt ist oder nicht. Quine-Paare können auch in typfreien Mengenlehre-Systemen als Klassenpaare fungieren.

Jedes Objekt ist ein Paar

1946 ist Quine eine weitere erstaunliche Eigenschaft seiner Paar-Definition aufgefallen: Jedes beliebige Objekt ist identisch zu einem geordnetem Paar. Für jedes Objekt $o$ gilt folgende Beziehung:

$\begin{array}{rcl}o& =& \{\theta (z):\theta (z)\in o\}\cup \{\theta (z)\cup \{0\}:\theta (z)\cup \{0\}\in o\}\\ & =& \{\theta (z):z\in \{z|\theta (z)\in o\}\}\cup \{\theta (z)\cup \{0\}:z\in \{z|\theta (z)\cup \{0\}\in o\}\}\\ & =& [\{z|\theta (z)\in o\},\{z|\theta (z)\cup \{0\}\in o\}]\end{array}$

Beispielsweise gilt, wenn man Quines Definition $0:=\{\mathrm{\varnothing }\}$ zugrunde legt:

$\mathrm{\varnothing }$	$=$	$[\mathrm{\varnothing },\mathrm{\varnothing }]$
$0$	$=$	$[0,\mathrm{\varnothing }]$	($0=\{\mathrm{\varnothing }\}=[\{\mathrm{\varnothing }\},\mathrm{\varnothing }]=[0,\mathrm{\varnothing }]$, da $\theta (\mathrm{\varnothing })=\mathrm{\varnothing }\in \{\mathrm{\varnothing }\}$)
$\{0\}$	$=$	$[\mathrm{\varnothing },0]$	($\{0\}=\{\{\mathrm{\varnothing }\}\}=[\mathrm{\varnothing },\{\mathrm{\varnothing }\}]=[\mathrm{\varnothing },0]$, da $\theta (\mathrm{\varnothing })\cup 0=\mathrm{\varnothing }\cup \{\mathrm{\varnothing }\}=\{\mathrm{\varnothing }\}\in \{\{\mathrm{\varnothing }\}\}$)

Quine merkt dazu an, dass alles eins wird:

Indeed, everything comes to be at once an ordered pair, a class, and a relation.

Ob das eine wirklich vorteilhafte Zusatzeigenschaft dieser Paardefinition ist, sei dahingestellt.

Morse (1965)

Morse definiert geordnete Paare in zwei Schritten.

Zunächst definiert er die klassischen Kuratowski-Paare (d. h. Mengenpaare) samt zugehörigem kartesischem Produkt und einem speziellen Operator $s(\cdot )$:

$\begin{array}{rcll}(x,y)& :=& \{\{x\},\{x,y\}\}& \text{(2.56.0)}\\ a\times b& :=& \{(x,y):x\in a,y\in b\}& \text{(S. 59; eine explizite Definition fehlt)}\\ s(a)& :=& \{\mathrm{\varnothing }\}\cup \{\{x\}|x\in a\}& \text{(2.57.0)}\end{array}$

Im zweiten Schritt definiert er die eigentlichen Klassenpaare und die zugehörigen Projektionsoperatoren:

$\begin{array}{rcll}[a,b]& :=& (\{0\}\times s(a))\cup (\{\{0\}\}\times s(b))& \text{(2.57.1)}\\ & =& \{(0,x):x\in s(a)\}\cup \{(1,x):x\in s(b)\}& \text{(2.131.0, 2.92.6,}1:=\{0\}\text{)}\\ {\pi }_1(p)& :=& \bigcup \{x|(0,x)\in p\}& \text{(2.57.6, 2.1.28, 2.56.4, 2.33.2)}\\ {\pi }_2(p)& :=& \bigcup \{x|(1,x)\in p\}& \text{(2.57.9, 2.1.28, 2.56.4, 2.33.2)}\end{array}$

Anmerkungen zur Definition von Morse

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Paaroperatoren:

$\begin{array}{rcl}{\pi }_1([a,b])& =& \bigcup \{x|(0,x)\in [a,b]\}\\ & =& \bigcup \{x|(0,x)\in \{(0,x):x\in s(a)\}\}\\ & =& \bigcup \{x\in s(a)\}\}\\ & =& \bigcup s(a)\\ & =& a& \text{(2.61.1)}\\ {\pi }_2([a,b])& =& \bigcup \{x|(1,x)\in [a,b]\}\\ & =& \bigcup \{x|(1,x)\in \{(1,x):x\in s(b)\}\}\\ & =& \bigcup \{x\in s(b)\}\}\\ & =& \bigcup s(b)\\ & =& b& \text{(2.61.1)}\end{array}$

Das Paaraxiom

Morses Definition erfüllt wie Quines Definition das Paaraxiom für alle Klassen (siehe Morse (1965), 2.61.2), d. h. für Mengen und für Unmengen, da die Paarelemente $a$ und $b$ nur rechts vom Elementsymbol $\in$ vorkommen. Kuratowski-Paare sind zwar nur für Mengen definiert, aber das zugehörige kartesische Produkt ist auch für Klassen definiert (beispielsweise ist $\mathrm{\Omega }\times \mathrm{\Omega }=\{(o_1,o_2):o_1,o_2\in \mathrm{\Omega }\}$ die Klasse aller Ordinalzahlpaare). Und auch der Operator $s$ ist für beliebige Klassen definiert.

Morses Symbole

Morse verwendet etwas andere Symbole, als zuvor angegeben:

• Anstelle von $(\cdot ,\cdot )$ und $[\cdot ,\cdot ]$ notiert er $({\cdot }_{´}\cdot )$ und $(\cdot ,\cdot )$.
• Die zugehörigen kartesischen Produkte notiert er jeweils zwei Kommas $(\cdot {}_{´}{}_{´}\cdot )$ und $(\cdot ,,\cdot )$.
• Die runden Klammern lässt er bei Paaren und kartesischen Produkten teilweise weg.
• Die Projektionsoperatoren heißen bei ihm ${\mathrm{c}\mathrm{r}\mathrm{d}}^{\prime }$ und ${\mathrm{c}\mathrm{r}\mathrm{d}}^{″}$.
• Die große Vereinigung bezeichnet er mit $▽$, den großen Durchschnitt mit $△$.

Die Idee hinter Morses Definition

Morse hat erkannt, dass sich das kartesische Produkt von klassischen Mengenpaaren zur Definition von geordneten Klassenpaaren eignet. (Er spricht – wie einige andere Mathematiker auch – von Wiener-Paaren, meint und verwendet jedoch Kuratowski-Paare.) Während $(a,b)$ nur für Mengen $a$ und $b$ definiert ist, ist $a\times b$ auch für Klassen definiert. Ein Problem ist allerdings, dass stets $a\times \mathrm{\varnothing }=\mathrm{\varnothing }\times b=\mathrm{\varnothing }$ gilt. Das heißt, das kartesische Produkt erfüllt das Paaraxiom für die leere Menge nicht.

J. W. Weihe, ein Ph.D.-Student von Morse, schlägt laut Morse 1949 vor, die Potenzmengen von $a$ und $b$ mittels des kartesischen Produktes zu verknüpfen, da die Potenzmenge nie leer ist:

$\begin{array}{rcl}[a,b]& :=& \mathcal{P}(a)\times \mathcal{P}(b)\end{array}$

1965 haben Morse und D. C. Peterson diese Idee verfeinert und anstelle von $\mathcal{P}(a)$ und $\mathcal{P}(b)$ die Klassen $s(a)$ und $s(b)$ verwendet. Der Operator $s$ ersetzt jedes Element $x$ der Klasse $a$ bzw. $b$ durch die einelementige Menge $\{x\}$. Damit $s(a)$ und $s(b)$ nicht leer sind, fügt Morse außerdem die leere Menge als Element hinzu. Die leere Menge ist das einzige nicht-einelementige Element von $s(a)$ und $s(b)$. Daher können $a$ und $b$ stets aus $s(a)$ und $s(b)$ rekonstruiert werden:

$\begin{array}{lcll}\bigcup s(a)& =& a& \text{(2.60.1)}\\ \bigcup s(b)& =& b& \text{(2.60.1)}\end{array}$

Einheit von Logik und Mengenlehre

In der obigen Definition und in den nachfolgenden Erklärungen werden jeweils in Klammern die Nummern bzw. Seiten der zugehörigen Definitionen von Morse (1965) angegeben. Der Grund ist, dass Anthony P. Morse Logik und Mengenlehre als Einheit auffasst und daher seine Formeln etwas schwerer zu lesen sind. Jede von Morse verwendete Formel kann sowohl prädikatenlogisch als auch mengentheoretisch interpretiert werden. Beispielsweise kann der Term $a\wedge b$ sowohl als logische Konjunktion der Aussagen $a$ und $b$, als auch als Durchschnitt der Klassen $a$ und $b$ interpretiert werden.

Auf den ersten Blick stimmen daher die obigen Definitionen nicht mit den Definitionen von Morse überein. Morse definiert $s(a)$ beispielsweise folgendermaßen (er verwendet überdies $ss$ an Stelle von $s$):

$\begin{array}{rc}s(a)\equiv (\mathrm{s}\mathrm{n}\mathrm{g}0\cup \bigvee \mathrm{x}(\mathrm{x}\in \mathrm{a}\wedge \mathrm{s}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{n}\mathrm{g}\mathrm{x}))& \text{(2.57.0)}\end{array}$

Dass diese Definition von Morse mit der oben angegeben Definition übereistimmt, sieht man folgendermaßen:

Das Symbol $\equiv$ bedeutet bei Morse „definitionsgemäß äquivalent zu“ (“Foreword”, S. xii). Es kann aber auch als $=$, d. h. als „(definitionsgemäß) gleich zu“ aufgefasst werden (2.4, “axiom of definition for set theory”), wobei $=$ für Klassen auf die übliche Weise definiert wird:

$\begin{array}{rr}(x=y)\equiv ((x\subset y)\wedge (y\subset x))& \text{(2.3.1)}\end{array}$

Für eine Menge $x$ (d. h. $x\in U$, wobei $U$ bei Morse die Allklasse ist) gilt $\mathrm{s}\mathrm{n}\mathrm{g}\mathrm{x}=\{\mathrm{x}\}$ (2.55.0, 2.54.1). $\mathrm{s}\mathrm{n}\mathrm{g}\mathrm{x}$ bezeichnet also die einelementige Menge. Das heißt, Morses Definition ist äquivalent zu:

$\begin{array}{r}s(a)=\{0\}\cup \bigvee x(x\in a\wedge \{\{x\}\})\end{array}$

Die Zusammenfassung aller Mengen $x$, die das Prädikat $ux$ erfüllen, definiert Morse folgendermaßen:

$\begin{array}{rcll}\{x|ux\}& \equiv & \mathsf{E}xux& (2.33.2)\\ & \equiv & \bigvee x(0\in ux\wedge \mathrm{s}\mathrm{n}\mathrm{g}\mathrm{x})& \text{(2.33.0)}\\ & \equiv & \bigvee x(ux\wedge \{x\})& \text{(2.5.0, 2.55.0, 2.54.1)}\end{array}$

Die Klasse aller $x$, die $ux$ erfüllen, ist laut Morse also die große Vereinigung (vgl. 2.1.28, 2.1.29) aller einelementigen Mengen $\{x\}$, für die $x$ zusätzlich die Bedingung $ux$ erfüllt. Entsprechend ist $\bigvee x(x\in a\wedge \{\{x\}\})$ die Vereinigung aller $\{\{x\}\}$, für die $x$ die Bedingung $x\in a$ erfüllt. (Eine explizite Definition für diese Art der Verallgemeinerung des Mengenoperators $\{\cdot :\cdot \}$ hat Morse allerdings nicht angegeben.) Es gilt also:

$\begin{array}{l}\bigvee x(x\in a\wedge \{\{x\}\})=\{\{x\}|x\in a\}\end{array}$

und damit nicht nur in moderner Schreibweise, sondern auch in der Notation von Morse:

$\begin{array}{l}s(a)=\{\mathrm{\varnothing }\}\cup \{\{x\}:x\in a\}\end{array}$

Schmidt (1966)

Jürgen Schmidt definiert seine Klassenpaare „in Anlehnung an Quine“. Er kombiniert die Definition von Wiener mit der Idee von Quine, nicht $a$ und $b$, sondern deren Elemente im Paar zu vereinen:

$\begin{array}{rclcl}[a,b]& =& \{\{\{x\}\}:x\in a\}\cup \{\mathcal{P}(\{x\}):x\in b\}& =& \{\{\{x\}\}:x\in a\}\cup \{\{\mathrm{\varnothing },\{x\}\}:x\in b\}\\ {\pi }_1(p)& =& \{x|\{\{x\}\}\in p\}\\ {\pi }_2(p)& =& \{x|\{\mathrm{\varnothing },\{x\}\}\in p\}\end{array}$

Anmerkungen zur Definition von Schmidt

Bei ${\pi }_1$ und ${\pi }_2$ handelt es sich tatsächlich um Paaroperatoren:

$\begin{array}{rcl}{\pi }_1([a,b])& =& \{x|\{\{x\}\}\in [a,b]\}\\ & =& \{x|\{\{x\}\}\in (\{\{\{x\}\}:x\in a\}\cup \{\{\mathrm{\varnothing },\{x\}\}:x\in b\})\}\\ & =& \{x|\{\{x\}\}\in \{\{\{x\}\}:x\in a\}\}\\ & =& \{x|x\in a\}\\ & =& a\\ {\pi }_2([a,b])& =& \{x|\{\mathrm{\varnothing },\{x\}\}\in [a,b]\}\\ & =& \{x|\{\mathrm{\varnothing },\{x\}\}\in (\{\{\{x\}\}:x\in a\}\cup \{\{\mathrm{\varnothing },\{x\}\}:x\in b\})\}\\ & =& \{x|\{\mathrm{\varnothing },\{x\}\}\in \{\{\mathrm{\varnothing },\{x\}\}:x\in b\}\}\\ & =& \{x|x\in b\}\\ & =& b\end{array}$

Man beachte, dass auch in der Definition von Schmidt $a$ und $b$ nur rechts von $\in$ stehen. Für Schmidt-Paare gilt daher das Paaraxiom ebenso wie für Quine- und Morse-Paare uneingeschränkt sowohl für Mengen als auch für Unmengen.

Oberschelp und Todt (1981)

TO BE DONE

Die wichtigsten axiomatischen Definitionen

Peano (1897)

Definition des geordneten Paars und Paaraxiom, Peano (1897a), S. 580

$(x;y)$ indica la coppia formata dagli oggetti $x$ ed $y$.

Questa coppia è considerata come un nuovo oggetto. [...]

L'idea di coppia è fondamentale, cioè noi non la sappiamo esprimere mediante i simboli precedenti. Però possiamo definire l'eguaglianza di due coppie:

[...]$(x;y)=(a;b).=.x=a.y=b$ Def.

“ la coppia $(x;y)$ dicesi eguale alla $(a;b)$, quando i loro elementi sono ordinatamente eguali „.

Übersetzung und angepasste Symbolik (Kowarschick)

$(x;y)$ bezeichnet das Paar, das aus den Objekten $x$ und $y$ gebildet wird.

Dieses Paar wird als neues Objekt betrachtet. [...]

Die Idee eines geordneten Zahlenpaars ist von grundlegender Bedeutung. Wir wissen aber nicht, wie wir es durch die [im Aufsatz] zuvor erwähnten Symbole ausdrücken können. Aber wir können die Gleichheit von zwei Paaren definieren:

[...]$(x;y)=(a;b):\iff x=a\mathrm{\&}y=b$

Das Paar $(x;y)$ ist gleich $(a;b)$, wenn ihre Elemente gemäß ihrer Anordnung gleich sind.

Neumann (1925)

TO BE DONE

McCarthy (1960)

In LISP werden geordnete Paare in der Form $(a\cdot b)$ bzw. (a . b) (ASCII-Schreibweise) notiert und mit der Funktion cons erzeugt. Die Operatoren ${\pi }_1$ und ${\pi }_2$ zur Extraktion der Elemente heißen bei McCarthy car und cdr.

Listen werden in LISP als Abkürzung für cons-Ketten definiert (siehe Tupel, Abschnitt „Definition ‚List‘ (McCarthy (1960))“).

Paare und Tupel in der Informatik

Sowohl in der Mathematik als auch in der Informatik ist es von zentraler Bedeutung, unterschiedliche Objekte in „Containern“ zusammenzufassen.

In der Mathematik wird i. Allg. folgender Weg gewählt:

• Als „Basis-Container“ werden Mengen oder Klassen benutzt. Wie diese erzeugt werden, wird axiomatisch festgelegt. In diesen Containern sind die Elemente ungeordnet und jeweils höchstens einmal enthalten.
• In einem zweiten Schritt werden „geordnete Paare“ definiert.
• Auf Basis der geordneten Paar können in einem dritten Schritt Tupel definiert werden: In diesen Containern sind die Elemente geordnet und evtl. auch mehrfach enthalten.

In der Informatik wird dagegen i. Allg. der umgekehrte Weg gewählt:

• Als „Basis-Container“ werden geordnete Paare oder Tupel bzw. Arrays, die als Verallgemeinerung des Paar-Begriffs aufgefasst werden können, benutzt. Wie diese erzeugt werden können, wird algorithmisch festgelegt. In diesen Containern sind die Elemente geordnet und evtl. auch mehrfach enthalten. Beispiele für derartige Basis-Container sind:
  • LISP: geordnete Paare („CONS-Zellen“, siehe den nachfolgenden Abschnitt „McCarthy (1960)“) sowie aus CONS-Zellen gebildete Listen (siehe den Absatz „Ursprung und Varianten der Vektornotation“ im Dokument Tupel); Konstruktoren: (a . b), (CONS A B)
  • C: Verbünde (record, Tupel; Schlüsselwort: struct) und Arrays
  • C++: zu Objekten verallgemeinerte Verbünde (Schlüsselwörter: struct, class) und Arrays
  • PASCAL: Verbünde (Schlüsselwort: RECORD) und Arrays
  • JavaScript: Objekte (Konstruktor: {a: Wert1, b: Wert2, ...}) und Arrays (Konstruktor: [a, b, c, ...])
  • etc.
• In einem zweiten Schritt können Mengen und auch Multimengen (das sind Container ohne Ordnung, in denen ein Element mehrfach enthalten sein kann) algorithmisch mit Hilfe der durch dies Sprache vorgegebenen Datenstrukturen definiert werden.

Eine Ausnahme bildet die Sprache SQL. Hier sind Tupel und Mengen (genauer: Multimengen) die zentralen Datenstrukturen zur Speicherung von Daten. In diesem Fall werden weder Mengen mit Hilfe von Tupeln noch Tupel mit Hilfe von Mengen nachgebildet.

Tupel als Mengen- oder Klassenpaare (Kowarschick (1991))

Der Tupelbegiff ist eine Verallgemeinerung des Paarbegriffs, der es ermöglicht, beliebig viele Elemente in einer geordneten Liste zusmmenzufassen. Wenn bereits der Tupelbegriff eingeführt wurde, kann man anschließend eine altenative Definition für geordnete Paare angeben:

$[a,b]:=(a,b)$ wobei $(a,b)$ ein $2$-Tupel ist.

Diese Definition klingt wie ein „circulus vitiosus“, da Tupel häufig mit Hilfe von Paaren definiert werden. Es liegt allerdings kein unzulässiger Ringschluss vor, da es für die Definition von Relationen, Funktionen etc. nur darauf ankommt, dass der gewählte Paaroperator das Paaraxiom erfüllt. Wie genau der Paaroperator definiert wurde, ist dabei ohne Belang.

Beispielsweise kann man $n$-Tupel – wie von John McCarthy für die Programmiersprache LISP vorgeschlagen – folgendermaßen definieren:

$0$-Tupel: $():=\mathrm{\varnothing }$

$1$-Tupel: $(a):=[a,\mathrm{\varnothing }]$

$2$-Tupel: $(a,b):=[a,[b,\mathrm{\varnothing }]]$

$3$-Tupel: $(a,b,c):=[a,[b,[c,\mathrm{\varnothing }]]]$

etc.

Kowarschick schlägt daher 1991 folgende induktive Definition für $n$-Tupel vor:

$0$-Tupel: $():=\mathrm{\varnothing }$

$n$-Tupel: $(a_1,\dots ,a_n):=[a_1,(a_2,\dots ,a_n)]$ für $n>0$

Dabei kann $[\cdot ,\cdot ]$ ein beliebiger Paaroperator sein (Kowarschick verwendet Schmidt-Paare). Falls es sich um einen Klassenpaar-Operator handelt, sind die $n$-Tupel ebenfalls sowohl für Mengen als auch für Unmengen definiert.

Insbesondere wird auf diese Weise ein neuer Paaroperator definiert: der $2$-Tupel-Operator $(\cdot ,\cdot )$. Er unterscheidet sich i. Allg. vom Paaroperator $[\cdot ,\cdot ]$, da $(a,b)=[a,[b,\mathrm{\varnothing }]]\ne [a,b]$ (zumindest sofern der Paar-Operator so definiert wurde, dass $[b,\mathrm{\varnothing }]\ne b$; dies ist bei den in diesem Artikel vorgestellten Paar-Operatoren nur bei den Quine-1945-Paaren nicht der Fall). Aber der $2$-Tupel-Operator erfüllt das Paaraxiom. Und dies ist – wie Dipert betont hat – die einzige Eigenschaft, auf die es beim Paarbegriff ankommt.

Daher geht man bei der Formalisierung der Mathematik sinnvollerweise folgendermaßen vor:

Entweder, man wählt eine Paar-Definition, die sich problemlos für beliebige Tupel verallgemeinern lässt (dies ist z. B. bei Quine- oder Morse-Paaren der Fall), oder man beschreitet folgenden Weg:

1. Man wählt eine beliebige Definition für Klassen- bzw. Mengenpaare (je nach dem benutzten Axiomensystem) zur Definition des Paaroperators $[\cdot ,\cdot ]$.
2. Man definiert $n$-Tupel (a_1,...,a_n) mit Hilfe dieser Paardefinition.
3. Man ignoriert ab nun den ursprünglichen Paaroperator $[.,.]$ und verwendet stattdessen den Paaroperator $(.,.)$ oder – allgemeiner – die Tupeloperatoren $(.,\cdots ,.)$, um weitere Grundbegriffe wie Kartesisches Produkt, Relation, Funktion etc. zu definieren.

Dass dieser Weg gangbar ist, hat Morse gezeigt, dessen Paardefinition ebenfalls zweistufig ist.

Siehe auch

• Projektion
• Scott, McCarty (2008): Dana Scott und Dominic McCarty; Reconsidering Ordered Pairs; in: The Bulletin of Symbolic Logic; Band: 14; Nummer: 3; Seite(n): 150-153; Verlag: Association for Symbolic Logic; Web-Link; 2008; Quellengüte: 5 (Artikel)